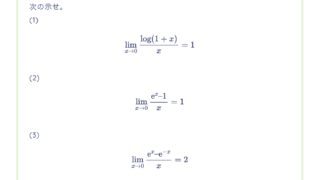
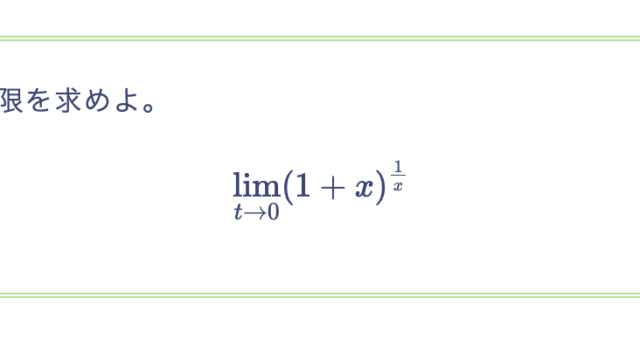次の方程式を解け。
(1)
\begin{align}
\arccos \frac{3}{5} &= \arcsin x
\end{align}
(2)
\begin{align}
\arcsin\frac{5}{13} + \arcsin\frac{4}{5} &= \arccos x
\end{align}
(1)
$\alpha = \arccos\frac{3}{5}$ とおくと、$\cos \alpha = \frac{3}{5}$ であり
\begin{align}
x &= \sin\alpha \\
&= \sqrt{1 – \cos^2 \alpha} \\
&= \frac{4}{5}
\end{align}
(2)
$\alpha = \arcsin\frac{5}{13}, \beta = \arcsin\frac{4}{5}$ とおくと
\begin{align}
\sin \alpha = \frac{5}{13},\ \cos \alpha = \frac{12}{13} \\
\sin \beta = \frac{4}{5},\ \cos \beta = \frac{3}{5}
\end{align}
$\alpha + \beta = \arccos x$ より
\begin{align}
x &= \cos(\alpha + \beta) \\
&= \cos \alpha \cos \beta – \sin\alpha \sin\beta \\
&= \frac{16}{65}
\end{align}