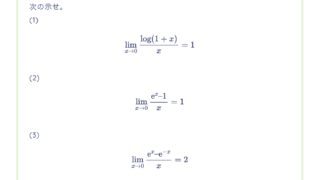
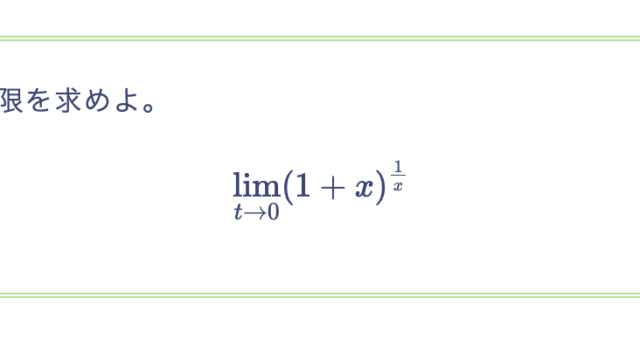次の値を求めよ。
(1)
\begin{align}
\arcsin(-1)
\end{align}
(2)
\begin{align}
\arcsin\left(- \frac{\sqrt{3}}{2}\right)
\end{align}
(3)
\begin{align}
\arccos\frac{1}{2}
\end{align}
(4)
\begin{align}
\arccos\frac{\sqrt{3}}{2}
\end{align}
(5)
\begin{align}
\arccos\left(\sin\frac{\pi}{6}\right)
\end{align}
(6)
\begin{align}
\arctan\frac{\sqrt{3}}{3}
\end{align}
(1)
\begin{align}
\arcsin(-1) &= – \frac{\pi}{2}
\end{align}
(2)
\begin{align}
\arcsin\left(- \frac{3}{2}\right) &= – \frac{\pi}{3}
\end{align}
(3)
\begin{align}
\arccos\frac{1}{2} &= \frac{\pi}{3}
\end{align}
(4)
\begin{align}
\arccos\frac{\sqrt{3}}{2} &= \frac{\pi}{6}
\end{align}
(5)
\begin{align}
\arccos\left(\sin\frac{\pi}{6}\right) &= \frac{\pi}{3}
\end{align}
(6)
\begin{align}
\arctan\frac{\sqrt{3}}{3} &= \frac{\pi}{6}
\end{align}