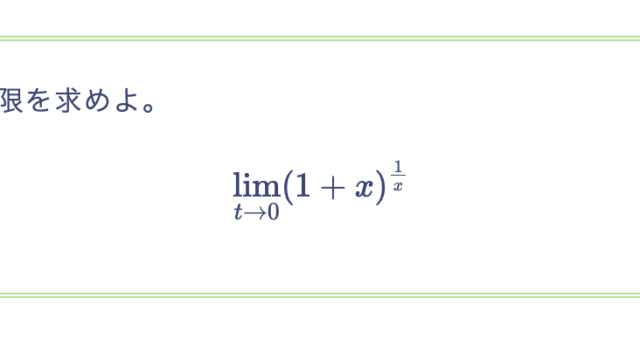実数 $a, b$ に対して、次を示せ。
(1)
\begin{align}
||a| – |b|| \le |a \pm b| \le |a| + |b|
\end{align}
(2)
\begin{align}
{\rm max}\{a, b\} = \frac{a + b + |a – b|}{2}
\end{align}
(3)
\begin{align}
{\rm min}\{a, b\} = \frac{a + b – |a – b|}{2}
\end{align}
(1)
\begin{align}
– |a| &\le a \le |a| \\
– |b| &\le b \le |b|
\end{align}
より
\begin{align}
– (|a| + |b|) &\le a + b \le |a| + |b|
\end{align}
が導かれるので
\begin{align}
|a + b| \le |a| + |b|
\end{align}
が得られる。さらに $b$ を $-b$ として
\begin{align}
|a – b| \le |a| + |b|
\end{align}
が得られ、さらに
\begin{align}
|a| = |(a – b) + b| \le |a – b| + |b|
\end{align}
より
\begin{align}
|a| – |b| \le |a – b|
\end{align}
が得られる。また、$a$ と $b$ を入れ替えて
\begin{align}
|b| – |a| \le |a – b|
\end{align}
が得られるので
\begin{align}
||a| – |b|| \le |a – b|
\end{align}
が導かれる。これにより、示すべき式が示された。
(2)
$a \ge b$ と仮定すると、左辺は $a$ であり、右辺は
\begin{align}
\frac{a + b + |a – b|}{2} &= \frac{a + b + a – b}{2} = a
\end{align}
となり、等しいことが分かる。$a \le b$ の場合も全く同様に示される。
(3)
$a \ge b$ と仮定すると、左辺は $b$ であり、右辺は
\begin{align}
\frac{a + b – |a – b|}{2} &= \frac{a + b – (a – b)}{2} = b
\end{align}
となり等しいことが分かる。$a \le b$ の時も全く同様に示される。