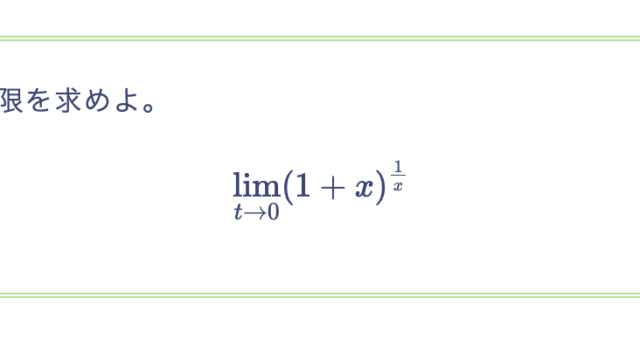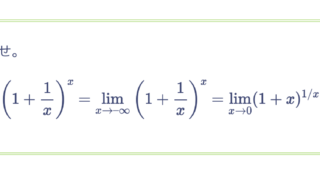関数の極限(4)

(1)
$a \neq 0$ の場合、$t = ax$ とおくと
\begin{align}
\lim_{x \to 0}(1 + ax)^1/x &= \lim_{x \to 0}\left(\left(1 + ax\right)^{\frac{1}{a x}}\right)^a \\
&= {\rm e}^a
\end{align}
となる。また、$a = 0$ の時には
\begin{align}
\lim_{x \to 0} (1 + a x)^{1/x} = 1 = {\rm e}^a
\end{align}
である。従って
\begin{align}
\lim_{x \to 0}(1 + a x)^{1/x} = {\rm e}^a
\end{align}
が言える。
(2)
$t = x – 1$ とおくと
\begin{align}
\lim_{x \to 1} x^{\frac{1}{x – 1}} &= \lim_{t \to 0}(1 + t)^{\frac{1}{t}} \\
&= {\rm e}
\end{align}
が言える。
(3)
$a \neq 0$ の時、$a/x = t$ とおくと
\begin{align}
\lim_{x \to \infty}\left(1 + \frac{a}{x}\right)^x &= \lim_{t \to 0}(1 + t)^{\frac{a}{t}} \\
&= {\rm e}^a
\end{align}
となり、$a =0$ の時には
\begin{align}
\lim_{x \to \infty}\left(1 + \frac{a}{x}\right)^x &= 1 = {\rm e}^a
\end{align}
であるので、結局
\begin{align}
\lim_{x \to \infty}\left(1 + \frac{a}{x}\right)^x &= {\rm e}^a
\end{align}
が言える。
(4)
$t = x – a$ とおいて
\begin{align}
\lim_{x \to a}\frac{\sin x – \sin a}{x – a} &= \lim_{t \to 0}\frac{\sin(t + a) – \sin a}{t} \\
&= \lim_{t \to 0}\frac{2 \sin\frac{t}{2} \cos\left(\frac{t}{2} + a\right)}{t} \\
&= \cos a
\end{align}
となる。