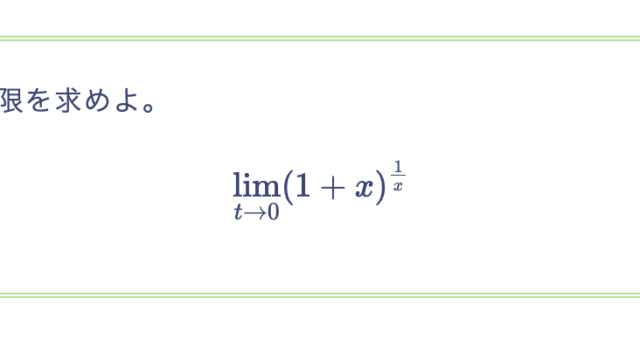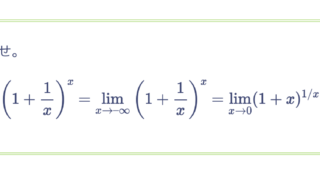次の関数の定義域と連続性を調べよ。
(1)
\begin{align}
f(x) &= \sin\left(\frac{x^3 + 1}{x^2 – 4}\right)
\end{align}
(2)
\begin{align}
f(x) = {\rm exp}\left(\frac{x^2 + 1}{x}\right)
\end{align}
(3)
\begin{align}
f(x) =
\begin{cases}
\frac{\sin x}{x (\pi – x)} & (x \neq 0, \pi) \\
\frac{1}{\pi} & (x = 0, \pi) \\
\end{cases}
\end{align}
(4)
\begin{align}
f(x) =
\begin{cases}
\frac{1}{1 + {\rm e}^{1/x^2}} & (x \neq 0) \\
0 & (x = 0) \\
\end{cases}
\end{align}
(1) $\sin y$ は $\mathbb{R}$ 全体で定義される $y$ の連続関数である。
また
\begin{align}
y = \frac{x^3 + 1}{x^2 – 4}
\end{align}
は $x \neq \pm 2$ で定義される連続関数である。
従って、$f(x)$ は $x \neq 2$ で定義される連続関数である。
(2) ${\rm e}^y$ は $\mathbb{R}$ 全体で定義される連続関数である。
また
\begin{align}
y &= \frac{x^2 + 1}{x}
\end{align}
は $x \neq 0$ で定義される連続関数である。
従って、$f(x)$ は $x \neq 0$ で定義される連続関数である。
(3) $f(x)$ は $\mathbb{R}$ 全体で定義される関数である。
$x = 0, \pi$ における連続性を調べる。
\begin{align}
\lim_{x \to 0} \frac{\sin x}{x (\pi – x)} &= \frac{1}{\pi}
\end{align}
より、$x = 0$ において連続であることが分かる。
$x = \pi$ において、$t = x – \pi$ とおくと
\begin{align}
\lim_{x \to \pi} \frac{sin x}{x (\pi – x)} &= \lim_{t \to 0}\frac{\sin(t + \pi)}{- t} \frac{1}{\pi} \\
&= \frac{1}{\pi} \lim_{t \to 0} \frac{- \sin t}{- t} \\
&= \frac{1}{\pi}
\end{align}
となり、$x = \pi$ においても連続であることが分かる。
(4) $f(x)$ は $\mathbb{R}$ 全体で定義される関数である。
$x = 0$ における連続性を調べる。
\begin{align}
\lim_{x \to 0} \frac{1}{1 + {\rm e}^{1/x^2}} &= 0
\end{align}
より、$x = 0$ において連続であることが分かる。