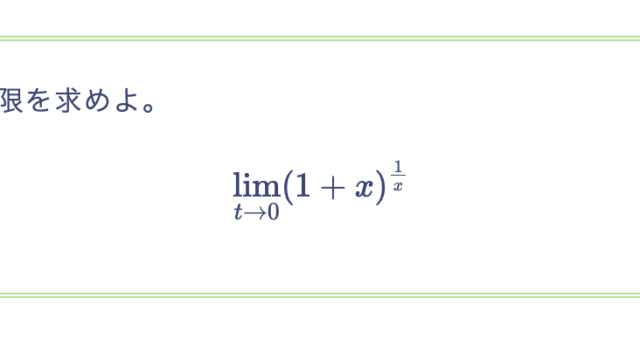次を示せ。
(1) $a > 0$ のとき
\begin{align}
\lim_{x \to \infty} a^x =
\begin{cases}
\infty & (a > 1) \\
1 & (a = 1) \\
0 & (o \le a < 1) \\
\end{cases}
\end{align}
(2)
$a > 1$ のとき
\begin{align}
\lim_{x \to 0} a^x = 1\ (a > 0)
\end{align}
先の問題より
\begin{align}
\lim_{n \to \infty} a^n = \infty
\end{align}
が分かっている。
今、$n \in \mathbb{N}$ を $n \le x < n + 1$ となるように取れば
\begin{align}
a^n \le a^x < a^{n + 1}
\end{align}
が言える。
ここで、$x \to \infty$ とすれば $n \to \infty$ となり、$a_n \to \infty, a^{n + 1} \to \infty$ となり
\begin{align}
\lim_{x \to \infty} a^x = \infty
\end{align}
が言える。
次に $a = 1$ の時には、明らかに
\begin{align}
\lim_{x \to \infty} a^x = 1
\end{align}
が成り立つ。
最後に $a < 1$ の時には、先の問題より
\begin{align}
\lim_{n \to \infty} a_n = 0
\end{align}
が分かっているので、$n \in \mathbb{N}$ を $n \le x < n + 1$ となるように取り
\begin{align}
a^n \ge a^x > a^{n + 1}
\end{align}
より、$x \to \infty$ で $n \to \infty$ となることと、両辺が 0 に収束するので
\begin{align}
\lim_{x \to \infty} a^x = 0
\end{align}
が言える。
(2)
$x \to +0$ とする。$1 > x > 0$ の時、$\frac{1}{n} \ge x > \frac{1}{n + 1}$ なる $n \in \mathbb{N}$ が存在する。
今、$x \to +0$ とすると $n \to \infty$ となり、$a > 1$ の場合には
\begin{align}
\lim_{n \to \infty} a^{\frac{1}{n}} \ge \lim_{x \to 0} a^x \ge \lim_{n \to \infty} a^{\frac{1}{n + 1}}
\end{align}
となり
\begin{align}
\lim_{x \to 0} a^x = 1
\end{align}
が言える。
ここで、先の結果を使った。
また、$1 > a > 0$ の場合には、不等号の向きが逆になり、やはり同じ結論が導かれる。
$x \to – 0$ の場合には
\begin{align}
\lim_{x \to -0} a^x &= \lim_{x \to +0} a^{- x} \\
&= \lim_{x \to + 0} \frac{1}{a^x} \\
&= 1
\end{align}
となる。
ここで、$x \to +0$ の場合の結果を使った。
従って、題意が示された。