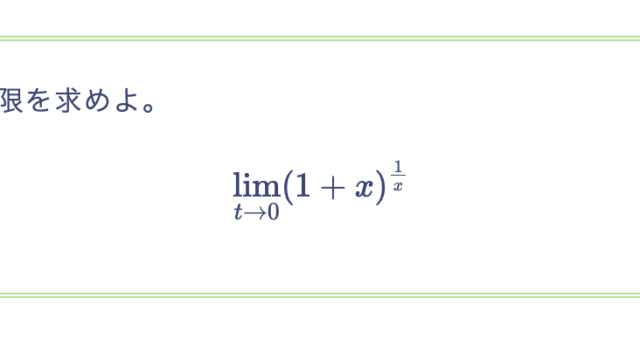次のように帰納的に定義される数列 $\{a_n\}$ の極限値を求めよ。
\begin{align}
(1) & a_1 = 1, a_{n + 1} = \frac{3 a_n + 2}{a_n + 1}\ (n \ge 1) \\
(2) & a_1 = 1, a_{n + 1} = \frac{1}{2}\left(a_n + \frac{3}{a_n}\right)\ (n \ge 1)\\
(3) & a_1 = 1, a_{n + 1} = \sqrt{a_n + 1}\ (n \ge 1)
\end{align}
(1)
まず、この数列の有界性を示す。すなわち $a_n < 3$ であることを示す。
$n = 1$ のときは $a_1 = 1 < 3$ より明らかに成り立っている。
次に $n > 2$ に対して
\begin{align}
a_{n + 1} &= \frac{3 a_n + 2}{a_n + 1} \\
&= 3 – \frac{1}{a_n + 1} < 3
\end{align}
より、任意の $n \in \mathbb{N}$ について $a_n < 3$ が成り立っていることが分かる。
ここで、$a_n > 0$ であることを用いた。
次に、この数列の単調性を示す。すなわち、単調増加数列であることを示す。
まず、$a_2 – a_1 = 3/2 > 0$ が成り立っている。
次に $n > 2$ に対して
\begin{align}
a_{n + 1} – a_n &= \frac{3 a_n + 2}{a_n + 1} – \frac{3 a_{n – 1} + 2}{a_{n – 1} + 1} \\
&= 2 \frac{a_n – a_{n – 1}}{(a_n + 1)(a_{n – 1} + 1)} > 0
\end{align}
が言えるので、単調増加数列であることが分かる。ここで $n = 2$ のときに上式の不等号が成り立つことを用いた。
従って、数列 $\{a_n\}$ は上に有界な単調増加数列であるので収束する。その収束値を $\alpha$ とすると
\begin{align}
\alpha &= \frac{3 \alpha + 2}{\alpha + 1} \\
\alpha &= 1 \pm \sqrt{3}
\end{align}
となり、今、$\alpha > 0$ より、$\alpha = 1 + \sqrt{3}$ と求まる。
(2)
まず、数列 $\{a_n\}$ の極限値が存在すると仮定すると
\begin{align}
\alpha &= \frac{1}{2}\left(\alpha + \frac{3}{\alpha}\right) \\
\alpha &= \pm \sqrt{3}
\end{align}
となり、$\alpha > 0$ を考慮して、$\alpha = \sqrt{3}$ と求まる。
以下、数列 $\{a_n\}$ が $\sqrt{3}$ に収束することを示す。
まず、相加相乗平均の関係より
\begin{align}
a_{n + 1} &= \frac{1}{2}\left(a_n + \frac{3}{a_n}\right) \ge \sqrt{3}
\end{align}
であることに注意する。
\begin{align}
a_{n + 1} – \sqrt{3} &= \frac{1}{2}\left(a_n + \frac{3}{a_n}\right) – \sqrt{3} \\
&= \frac{a_n – \sqrt{3}}{2 a_n} (a_n – \sqrt{3}) \ge 0
\end{align}
最後の不等式は先に相加相乗平均を用いて得られた関係を用いた。
さらに
\begin{align}
0 \le \frac{a_n – \sqrt{3}}{a_n} < 1
\end{align}
なる関係が成り立つことに注意して
\begin{align}
a_{n + 1} - \sqrt{3} &= \frac{1}{2} \frac{a_n - \sqrt{3}}{a_n} (a_n - \sqrt{3}) \\
&\le \frac{1}{2}(a_n - \sqrt{3}) \\
&\le \left(\frac{1}{2}\right)^2 (a_{n - 1} - \sqrt{3}) \\
&\le \left(\frac{1}{2}\right)^n (a_1 - \sqrt{3})
\end{align}
が成り立つので
\begin{align}
\lim_{n \to ]infty} |a_n - \sqrt{3}| = 0
\end{align}
が言える。従って、数列 $\{a_n\}$ は $\sqrt{3}$ に収束することが分かる。
(3)
まず、数列 $\{a_n\}$ の有界性を示す。すなわち,$a_n < 2$ を示す。
数学的帰納法を用いて示す。
まず、$a_1 = 1 < 2$ である。
次に、$a_n < 2$ と仮定すると
\begin{align}
a_{n + 1} &= \sqrt{a_n + 1} < \sqrt{2 + 1} < 2
\end{align}
となり、$a_{n + 1} < 2$ が示される。
次に、数列 $\{a_n\}$ が単調増加数列であることを、同様に数学的帰納法により示す。
まず、$a_1 = 1, a_2 = \sqrt{2}$ より $a_1 < a_2$ が成り立っている。
次に $a_n > a_{n – 1}$ が成り立っているとするとき
\begin{align}
a_{n + 1} – a_n &= \sqrt{a_n + 1} – \sqrt{a_{n – 1} + 1} \\
&= (\sqrt{a_n + 1} – \sqrt{a_{n – 1} + 1})\frac{\sqrt{a_n + 1} + \sqrt{a_{n – 1} + 1}}{\sqrt{a_n + 1} + \sqrt{a_{n – 1} + 1}} \\
&= \frac{a_n – a_{n – 1}}{\sqrt{a_n + 1} + \sqrt{a_{n – 1} + 1}} > 0
\end{align}
が成立する。
従って、数列 $\{a_n\}$ は上に有界な単調増加数列であるので、極限値を持つ。その極限値を $\alpha$ とすると
\begin{align}
\alpha &= \sqrt{\alpha + 1} \\
\alpha &= \frac{1 \pm \sqrt{5}}{2}
\end{align}
となり、$\alpha > 0$ に注意すると、極限値は
\begin{align}
\frac{1 + \sqrt{5}}{2}
\end{align}
と求まる。