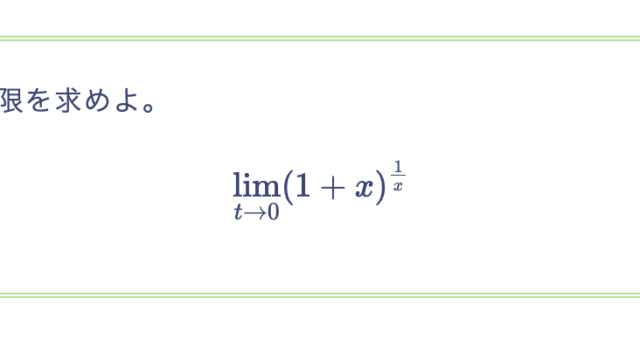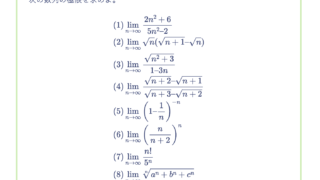数列の極限(1)

(1)
$a > 1$ のときには、$a = 1 + h\ (h > 0)$ とおくことが出来て、二項定理より
\begin{align}
a^n &= (1 + h)^n\\
&=1 + n h + \frac{n(n – 1)}{2} n^2 + \cdots + n^n \\
& \ge 1 + nh
\end{align}
が示される。ここで、アルキメデスの原理より
\begin{align}
n h \to \infty
\end{align}
が言えるので
\begin{align}
\lim_{n \to \infty} a^n = \infty
\end{align}
となる。

次に $a = 1$ のときには、任意の $n \in \mathbb{N}$ に対して、$a^n = 1$ であるので、明らかに
\begin{align}
\lim_{n \to \infty} a^n = 1
\end{align}
が言える。

最後に $a < 1$ の時には、$b = \frac{1}{a} > 1$ として、最初の結果より
\begin{align}
\lim_{n \to \infty} b^n = \infty
\end{align}
が言える。従って
\begin{align}
\lim_{n \to \infty}a^n &= \lim_{n \to \infty} \frac{1}{b^n} \\
&= 0
\end{align}
が結論付けられる。

(2)
まず $a > 1$ とするとき、$a = 1 + h\ (h > 0)$ とおくことが出来て、二項定理より
\begin{align}
\left(1 + \frac{h}{n}\right)^n &= 1 + h + \frac{n (n – 1)}{2} \left(\frac{h}{n}\right)^2 + \cdots + \left(\frac{h}{n}\right)^n \\
&\ge 1 + h
\end{align}
が成り立つことに注意して
\begin{align}
\left(1 + \frac{h}{n}\right)^n &\ge 1 + h = a > 1
\end{align}
となるので
\begin{align}
1 + \frac{h}{n} \ge \sqrt[n]{a} \ge 1
\end{align}
が成り立つ。ここで、$n \to \infty$ の極限を取り、はさみうちの原理より
\begin{align}
\lim_{n \to \infty} \sqrt[n]{a} &= 1
\end{align}

次に $a = 1$ のときは、任意の $n \in \mathbb{N}$ に対して $\sqrt[n]{a} = 1$ より、明らかに
\begin{align}
\lim_{n \to \infty} \sqrt[n]{a} &= 1
\end{align}
が言える。

最後に、$a < 1$ のときは、$b = \frac{1}{a}$ とすれば、$b > 1$ の時の結果が使えて
\begin{align}
\lim_{n \to \infty} \sqrt[n]{a} &= \lim_{n \to \infty} \frac{1}{\sqrt[n]{b}} \\
&= 1
\end{align}
が言える。