$A, B$ を集合とするとき
(1) $A \bigtriangleup B := (A \backslash B) \cup (B \backslash A)$ を集合 $A, B$ の対称差という。これをベン図で図示せよ。
(2) 集合 $(A \bigtriangleup B) \bigtriangleup C$ と $A \bigtriangleup (B \bigtriangleup C)$ を各々図示し、両者が一致することを確かめよ。これは対称差が結合法則を満たすことを示している。
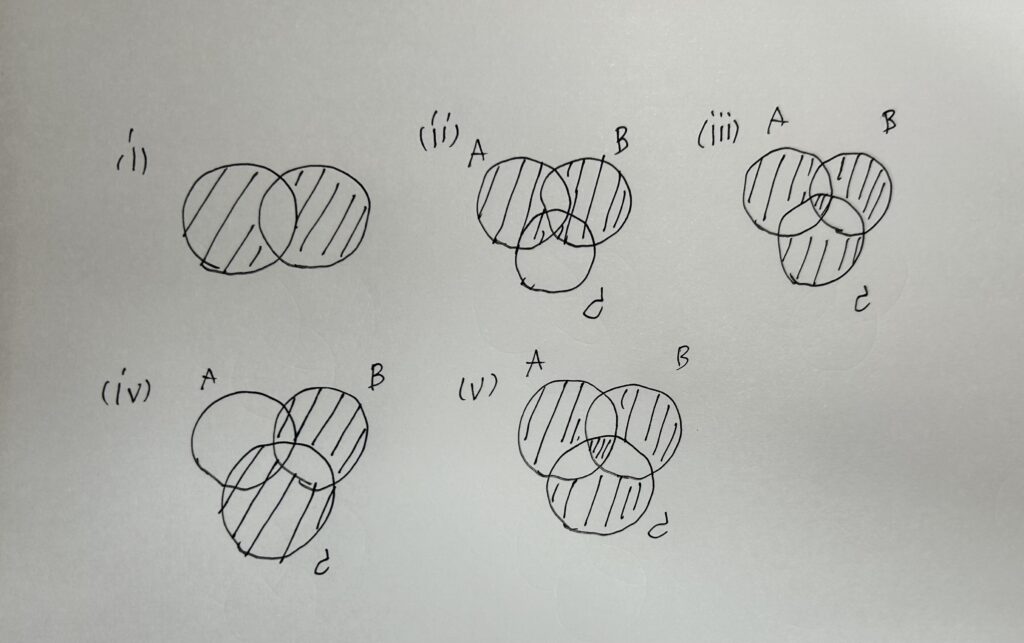
(1) 集合 $A, B$ の対称差は (i) のようにベン図の斜線部で表すことが出来る。
(2) $A \bigtriangleup B$ は (ii) の斜線部となる。
従って、$(A \bigtriangleup B) \bigtriangleup C$ は (iii)の斜線部となる。
一方で、$B \bigtriangleup C$ は (iv) の斜線部となるので、$A \bigtriangleup (B \bigtriangleup C)$ は (v) の斜線部となる。
従って、両者が等しいことが分かる。