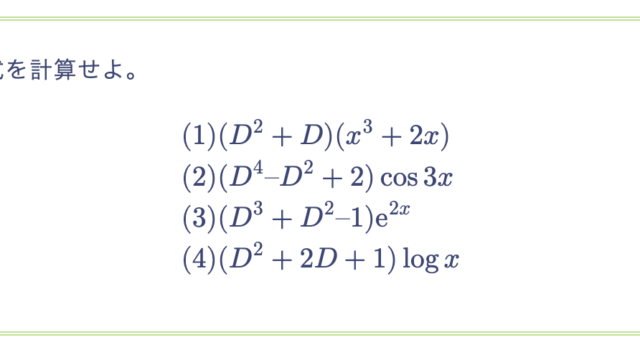高階完全微分方程式(2)

各係数を次のように置く。
\begin{align}
P_0 &= x^3 + x^2 + 2 x + 1 \\
P_1 &= 9 x^2 + 6 x + 6 \\
P_2 &= 18 x + 6 \\
P_3 &= 6
\end{align}

このとき、先の問題より
\begin{align}
P_3 – P_2′ + P”_1 – P”’_0 &= 6 – (18 +6)’ + (9 x^2 + 6 x + 6)” – (x^3 + x^2 + 2 x + 1)”’ \\
&= 0
\end{align}
であるので、解くべき微分方程式は完全微分方程式であることが分かる。
そこで、完全微分方程式を解く処方箋に従って
\begin{align}
q_0 &= P_0 = x^3 + x^2 + 2 x + 1 \\
q_1 &= P1 – P’_0 = (9 x^2 + 6 x + 6) – (x^3 + x^2 + 2 x + 1)’ \\
&= 6 x^2 + 4 x + 4 \\
q_2 &= P_2 – P’_1 + P”_0 = (18 x + 6) – (9 x^2 + 6 x + 6)’ + (x^3 + x^2 + 2 x + 1) \\
&= 6 x + 2
\end{align}
が得られるので
\begin{align}
q_0 y” + q_1 y’ + q_2 y &= \int 24 x {\rm d} x \\
(x^3 + x^2 + 2 x + 1) y” + (6 x^2 + 4 x + 4) y’ + (6x + 2) y &= 12 x^2 + C_1 \\
\end{align}
が得られる。そこで新たに
\begin{align}
P_0 &= x^3 + x^2 + 2 x + 1 \\
P_1 &= 6 x^2 + 4 x + 4 \\
P_2 &= 6 x + 2
\end{align}
と置くと
\begin{align}
P_2 – P’_1 + P”_0 &= (6 x + 2) – (6x^2 + 4 x + 4)’ (x^3 + x^2 + 2 x + 1)” \\
&= 0
\end{align}
となるので、この微分方程式も完全微分方程式であることが分かる。そこで
\begin{align}
q_0 &= P_0 = x^3 + x^2 + 2 x + 1 \\
q_1 &= P_1 – P’_0 = (6 x^2 + 4 x + 4) – (x^3 + x^2 + 2 x + 1)’ \\
&= 3 x^2 + 2 x + 2
\end{align}
であるので
\begin{align}
q_0 y’ + q_1 y &= \int (12 x^2 + C_1) {\rm d} x \\
(x^3 + x^2 + 2 x + 1) y’ + (3 x^2 + 2 x + 2) y &= 4 x^3 + C_1 x + C_2
\end{align}
が得られる。さらに、新たに
\begin{align}
P_0 &= x^3 + x^2 + 2 x + 1 \\
P_1 &= 3 x^2 + 2 x + 2
\end{align}
と置くと
\begin{align}
P_1 – P’_0 &= (3 x^2 + 2 x + 2) – (x^3 + x^2 + 2 x + 1)’ \\
&= 0
\end{align}
となり、これも完全微分方程式であることが分かる。
ここで
\begin{align}
q_0 &= P_0 = x^3 + x^2 + 2 x + 1
\end{align}
であるので
\begin{align}
q_0 y &= \int (4 x^3 + C_1 x + C_2) {\rm d} x \\
(x^3 + x^2 + 2 x + 1) y &= x^4 + C_1 x^3 + C_2 x + C_3
\end{align}
が得られる。従って
\begin{align}
(x^3 + x^2 + 2 x + 1) y &= x^4 + C_1 x^2 + C_2 x + C_3
\end{align}
が解として求まる。
なお、積分定数 $C_1, C_2, C_3$ は途中で定数倍に置き換えたものを新たに定義している。