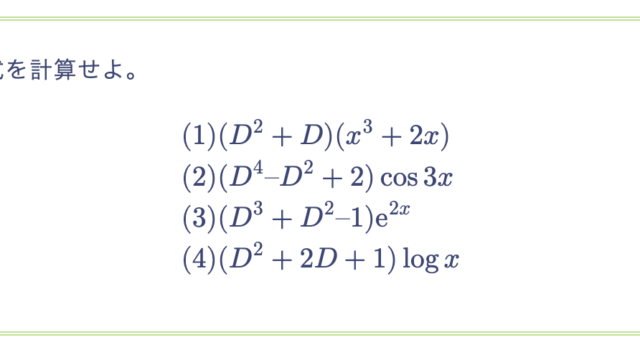$n$ 階線形微分方程式
\begin{align}
P_0 y^{(n)} + P_1 y^{(n – 1)} + P_2 y^{(n – 2)} + \cdots + P_{n – 1} y’ + P_n y &= R
\end{align}
が完全微分方程式となるための条件は
\begin{align}
P_n – P’_{n – 1} + P”_{n – 2} – P”’_{n – 3} + \cdots + (-1)^n P^{(n)}_0 &= 0
\end{align}
であることを示せ。
考えている微分方程式の両辺を $x$ で積分すると
\begin{align}
\int P_0 y^{(n)} {\rm d}x + \int P_1 y^{(n – 1)} {\rm d} x + \cdots + \int P_{n – 1} y’ {\rm d} x + \int P_n y {\rm d} x &= \int R {\rm d} x
\end{align}
が得られる。この式は各項を部分積分することにより簡略化することが出来る。実際に、左辺第1項は
\begin{align}
\int P_0 y^{(n)} {\rm d} x &= P_0 y^{(n – 1)} – \int P’_0 y^{(n – 1)} {\rm d} x \\
&= P_0 y^{(n – 1)} – P’_0 y^{(n – 2)} + \int P”_0 y^{(n – 2)} {\rm d} x \\
& \cdots \\
&= P_0 y^{(n – 1)} – P’_0 y^{(n – 2)} + \cdots + (-1)^{(n)} \int P^{(n)} y {\rm d} x
\end{align}
となる。これを各項行うことにより左辺は次の式に等しいことが分かる。
\begin{align}
& P_0 y^{(n – 1)} + (P_1 – P’_0) y^{(n – 2)} + (P_2 – P_1′ + P”_0) y^{(n – 3)} + \cdots +
\big(P_{n – 1} – P’_{n – 2} + \cdots \\
& \quad + (-1)^{n – 1} P_0^{(n – 1)}\big) y +
\int \big(P_n – P’_{n – 1} + P”_{n – 2} – \cdots + (-1)^{n – 1} P_1^{(n – 1)} + (-1)^n P_0^{(n)}\big) y {\rm d} x
\end{align}
従って、この最後の項の $\big(\cdots\big)$ 内がゼロであることが、求める微分方程式が完全微分方程式である条件であることがわかり、題意が証明された。