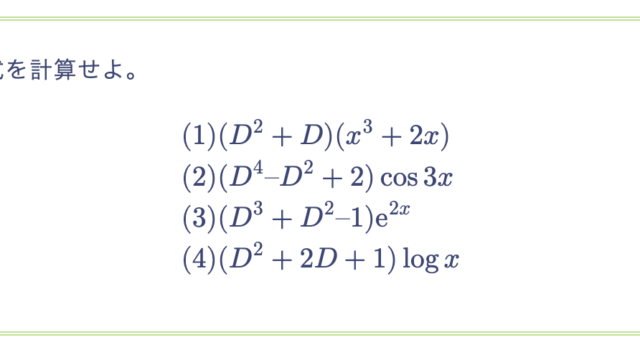高階微分方程式

与えられた微分方程式において $y’ = p$ とおくと
\begin{align}
p” – \frac{x}{x – 1} p’ + \frac{1}{x – 1} p &= 1 – x
\end{align}
となる。この $p$ についての2階の線形微分方程式の同伴方程式は
\begin{align}
p” – \frac{x}{x – 1} p’ + \frac{1}{x – 1} p &= 0
\end{align}
である。
これは
\begin{align}
P(x) &= – \frac{x}{x – 1} \\
Q(x) &= \frac{1}{x – 1}
\end{align}
とおくと
\begin{align}
p” + P(x) p’ + Q(x) p = 0
\end{align}
と表される。ここで $P(x), Q(x)$ は
\begin{align}
\begin{cases}
P(x) + x Q(x) &= 0 \\
1 + P(x) + Q(x) &= 0
\end{cases}
\end{align}
が成り立つので、先の結果より、同伴方程式の基本解は
\begin{align}
p_1 &= x \\
p_2 &= {\rm e}^x
\end{align}
であり、余関数 $Y$ は
\begin{align}
Y &= C_1 x + C_2 {\rm e}^x
\end{align}
と求まる。ここで $p_1$ と $p_2$ のロンスキアン $W(p_1, p_2)$ は
\begin{align}
W(p_1, p_2) &=
\begin{array}{|c c|}
p_1 & p_2 \\
p_1′ & p_2′ \\
\end{array} \\
&=
\begin{array}{|c c|}
x & {\rm e}^x \\
1 & {\rm e}^x \\
\end{array} \\
&= (x – 1) {\rm e}^x\ (\neq 0)
\end{align}
であり、$p_1, p_2$ は一次独立であることが確かめられたので、解くべき微分方程式の特殊解 $y_0$ は
\begin{align}
y_0 &= – x \int \frac{{\rm e}^x (1 – x)}{(x – 1) {\rm e}^x} {\rm d} x
+ {\rm e}^x \int \frac{x(1 – x)}{(x – 1){\rm e}^x} {\rm d} x \\
&= x \int {\rm d} x – {\rm e}^x \int x {\rm e}^{- x} {\rm d} x \\
&= x^2 + x + 1
\end{align}
と求まる。従って、$p$ は
\begin{align}
p &= x^2 + x + 1 + C_1 x + C_2 {\rm e}^x \\
&= x^2 + C_1′ x + 1 + C_2 {\rm e}^x
\end{align}
と求まる。従って $y’ = p$ に注意して、$p$ をもう一度積分することにより
\begin{align}
y &= \int (x^2 + C_1′ x + 1 + C_2 {\rm e}^x) {\rm d} x \\
&= \frac{1}{3} x^3 + C_1” x^2 _ x + C_2 {\rm e}^x + C_3
\end{align}
と一般解が求まる。ここで、$C_1”, C_2, C_3$ は任意定数である。