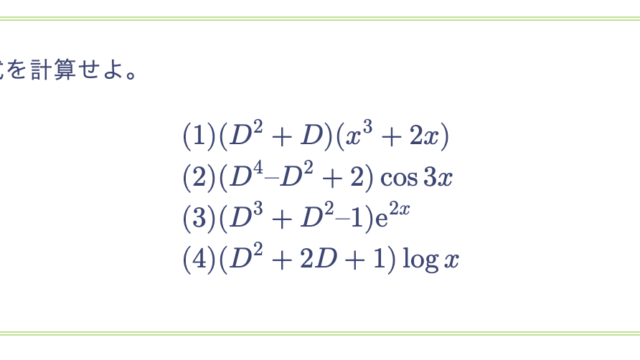次の微分方程式の一般解を求めよ。
\begin{align}
(1) & \quad x^3 y”’ – 3 x^2 y” + 7 x y’ – 8 y = x^2 \\
(2) & \quad x^4 y^{(4)} + 6 x^3 y”’ + 7 x^2 y” + x y’ – y = \sin(\log x)
\end{align}
まず、これらの微分方程式は、$y$ の微分の回数と同じ次数の $x$ がかかっていることに注意する。
これより $x = {\rm e}^t$ なる変数変換が思い付く。
(1)
$x = {\rm e}^t$ とおいて
\begin{align}
\frac{\rm d}{{\rm d} x} = D,\ \frac{\rm d}{{\rm d} t} = \delta
\end{align}
と書くことにすると
\begin{align}
x y’ &= x (D y) = \delta y \\
x^2 y” &= x^2 (D^2 y) = \delta (\delta – 1) y \\
x^3 y”’ &= x^3 (D^3 y) = \delta (\delta – 1) (\delta – 2) y
\end{align}
となる。
この関係式は、一般に
\begin{align}
x^n (D^n y) &= \delta (\delta – 1) (\delta – 2) \cdots (\delta – (n – 1)) y
\end{align}
が成り立つことから分かる。
従って、解くべき微分方程式は
\begin{align}
\big(\delta(\delta – 1)(\delta – 2) – 3 \delta(\delta – 1) + 7 \delta – 8\big)y &= {\rm e}^{2 t} \\
\big(\delta^3 – 6 \delta^2 + 12 \delta – 8\big) y &= {\rm e}^{2 t} \\
\big(\delta – 2\big)^3 &= {\rm e}^{2 t}
\end{align}
と変形出来る。この微分方程式の余関数 $Y$ は、特性方程式の解が $\lambda = 2\ {\text 3重解}$ であることより
\begin{align}
Y &= (C_1 + C_2 t + C_3 t^2) {\rm e}^{2 t}
\end{align}
と求まる。さらに、特殊解 $y_0$ は、先の結果を用いて
\begin{align}
y_0 &= \frac{1}{(\delta – 2)^3} {\rm e}^{2 t} \\
&= \frac{t^3}{3!} {\rm e}^{2 t} \\
&= \frac{1}{6} t^3 {\rm e}^{2 t}
\end{align}
と求まる。従って、求める一般解は
\begin{align}
y &= \frac{1}{6} t^3 {\rm e}^{2 t} + (C_1 + C_2 t + C_3 t^2){\rm e}^{2 t} \\
&= \frac{1}{6} (\log x)^3 x^2 + (C_1 + C_2 \log x + C_3 (\log x)^2) {\rm e}^2
\end{align}
となる。
(2)
(1) と同様に $x = {\rm e}^t$ とおき
\begin{align}
\frac{\rm d}{{\rm d} x} = D,\ \frac{\rm d}{{\rm d} t} = \delta
\end{align}
と書くことにすると、先の式
\begin{align}
x^n (D^n y) &= \delta (\delta – 1) (\delta – 2) \cdots (\delta – (n – 1)) y
\end{align}
より、解きたい微分方程式は
\begin{align}
\big(\delta(\delta – 1)(\delta – 2)(\delta – 3) + 6 \delta (\delta – 1) (\delta – 2) + 7 \delta (\delta – 1) + \delta – t\big) y &= \sin t \\
(\delta^4 – 1) y &= \sin t \\
(\delta – 1)(\delta + 1)(\delta^2 + 1) &= \sin t
\end{align}
と変形出来る。この微分方程式の余関数 $Y$ は、同伴方程式の特性方程式の解が $\lambda = \pm 1, \pm i$ であるので
\begin{align}
Y &= C_1 {\rm e}^t + C_2 {\rm e}^{- t} + C_3 \cos t + C_4 \sin t
\end{align}
と求まる。さらに、特殊解 $y_0$ は、先の結果を用いて
\begin{align}
y_0 &= \frac{1}{(\delta^2 + 1)(\delta^2 – 1)} \sin t \\
&= \frac{1}{\delta^2 + 1} \frac{\sin t}{- 1^2 – 1} \\
&= – \frac{1}{2} \frac{1}{\delta^2 + 1} \sin t \\
&= – \frac{1}{2} \bigg(- \frac{t \cos t}{2}\bigg) \\
&= \frac{1}{4} t \cos t
\end{align}
と求まる。従って、一般解は
\begin{align}
y &= \frac{1}{4} t \cos t + C_1 {\rm e}^t + C_2 {\rm e}^{- t} + C_3 \cos t + C_4 \sin t \\
&= \frac{1}{4}(\log x) \cos(\log x) + C_1 x + C_2 \frac{1}{x} + C_3 \cos(\log x) + C_4 \sin(\log x)
\end{align}
と求まる。