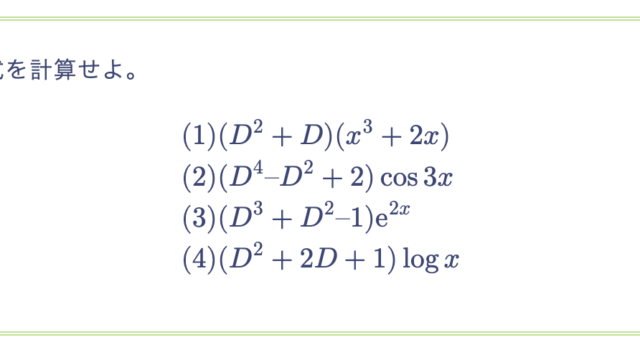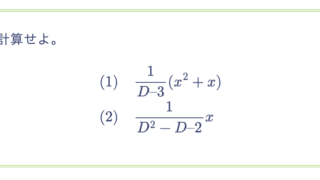次の各式が成り立つことを示せ。ただし、$\Phi(\lambda)$ は $\lambda$ の多項式
\begin{align}
\Phi(\lambda) &= \lambda^n + a_1 \lambda^{n – 1} + a_2 \lambda^{n – 2} + \cdots + a_{n – 1} \lambda + a_n
\end{align}
とする。
\begin{align}
(1) & \quad \frac{1}{\Phi(D^2)} \cos \alpha x = \frac{\cos \alpha x}{\Phi(- \alpha^2)} \\
(2) & \quad \frac{1}{D^2 + \alpha^2} \cos \alpha x = \frac{x \sin \alpha x}{2 \alpha}
\end{align}
(1)
先ず
\begin{align}
D^2 \cos \alpha x &= – \alpha^2 \cos \alpha x
\end{align}
に着目すれば
\begin{align}
D^{2 n} \cos \alpha x &= (- \alpha^2)^n \cos \alpha x
\end{align}
が分かる。ここで
\begin{align}
\Phi(D^2) &= D^{2n} + a_1 D^{2(n – 1)} + a_2 D^{2 (n – 2)} + \cdots + a_{n – 1} D^2 + a_n
\end{align}
とおくと
\begin{align}
\Phi(D^2) \cos \alpha x &= \big(D^{2n} + a_1 D^{2(n – 1)} + a_2 D^{2 (n – 2)} + \cdots + a_{n – 1} D^2 + a_n\big) \cos \alpha x \\
&= \big((- \alpha^2)^n + a_1 (- \alpha^2)^{n – 1} + a_2 (- \alpha^2)^{n – 2} + \cdots + a_{n – 1}(- \alpha^2) + a_n\big) \cos \alpha x \\
&= \Phi(- \alpha^2) \cos \alpha x
\end{align}
が成り立つ。従って
\begin{align}
\frac{1}{\Phi(D^2)} \cos \alpha x &= \frac{\cos \alpha x}{\Phi(- \alpha^2)}
\end{align}
が分かる。
(2)
\begin{align}
(D^2 + \alpha^2) x \sin \alpha x &= D^2 \big(x \sin \alpha x\big) + \alpha^2 x \sin \alpha x \\
&= 2 \alpha \cos \alpha x
\end{align}
より
\begin{align}
\frac{1}{D^2 + \alpha^2} \cos \alpha x &= \frac{x \sin \alpha x}{2 \alpha}
\end{align}
が得られる。