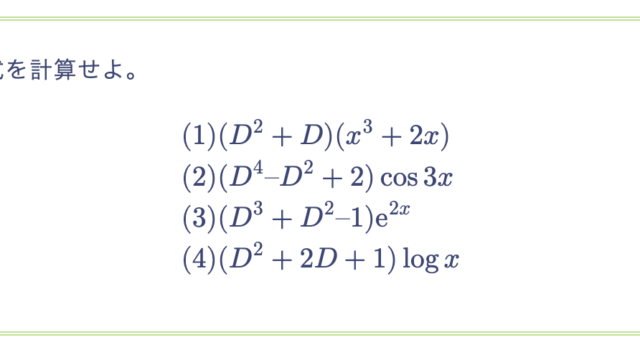次の各式が成り立つことを示せ。
ただし、$\Phi(\lambda)$ は $\lambda$ の多項式であり
\begin{align}
\Phi(\lambda) &= \lambda^n + a_1 \lambda^{n – 1} + a_2 \lambda^{n – 2} + \cdots + a_{n – 1} \lambda + a_n
\end{align}
とする。
\begin{align}
(1) & \quad \frac{1}{\Phi(D)} {\rm e}^{\alpha x} = \frac{e^{\alpha x}}{\Phi(\alpha)} \\
(2) & \quad \frac{1}{\Phi(D)}\Big({\rm e}^{\alpha x} f(x)\Big) = {\rm e}^{\alpha x} \frac{1}{\Phi(D + \alpha)} f(x) \\
(3) & \quad \frac{1}{D – \alpha} f(x) = {\rm e}^{\alpha x} \int {\rm e}^{- \alpha x} f(x) {\rm d} x \\
(4) & \quad \frac{1}{(D – \alpha)^n} {\rm e}^{\alpha x} = \frac{x^n}{n!} {\rm e}^{\alpha x}
\end{align}
(1)
先の結果より $D^n {\rm e}^{\alpha x} = \alpha^n {\rm e}^{\alpha x}$ が成り立つので
\begin{align}
\Phi(D) {\rm e}^{\alpha x} &= D^n {\rm e}^{\alpha x} + a_1 D^{n -1} {\rm e}^{\alpha x} + \cdots + a_{n – 1}D{\rm e}^{\alpha x} + a_n {\rm e}^{\alpha x} \\
&= \Big(\alpha^n + a_1 \alpha^{n – 1} + \cdots + a_{n – 1}\alpha + a_n\Big) {\rm e}^{\alpha x} \\
&= \Phi(\alpha) {\rm e}^{\alpha x}
\end{align}
が成立する。従って
\begin{align}
{\rm e}^{\alpha x} &= \frac{1}{\Phi(D)}\Big(\Phi(\alpha) {\rm e}^{\alpha x}\Big) \\
&= \Phi(\alpha) \frac{1}{\Phi(D)} {\rm e}^{\alpha x}
\end{align}
となり、$\Phi(\alpha) \neq 0$ とすると
\begin{align}
\frac{1}{\Phi(D)} {\rm e}^{\alpha x} &= \frac{e^{\alpha x}}{\Phi(\alpha)}
\end{align}
が成り立つ。
(2)
先の結果より、$D^n\big({\rm e}^{\alpha x} g(x)\big) = {\rm e}^{\alpha x} (D + \alpha)^n g(x)$ が成り立つので
\begin{align}
\Phi(D)\Big({\rm e}^{\alpha x} g(x)\Big) &= D^n\big({\rm e}^{\alpha x} g(x)\big) + a_1 D^{n – 1}\big({\rm e}^{\alpha x} g(x)\big) + \cdots + a_{n – 1} D\big({\rm e}^{\alpha x} g(x)\big) + a_n {\rm e}^{\alpha x} g(x) \\
&= {\rm e}^{\alpha x}\Big((D + \alpha)^n + a_1(D + \alpha)^{n – 1} + \cdots + a_{n – 1} (D – \alpha) + a_n\Big) g(x)\\
&= {\rm e}^{\alpha x} \Phi(D + \alpha) g(x)
\end{align}
が成り立つ。従って
\begin{align}
{\rm e}^{\alpha x} g(x) &= \frac{1}{\Phi(D)}\Big({\rm e}^{\alpha x} \Phi(D + \alpha) g(x)\Big)
\end{align}
が成立する。ここで $\Phi(D + \alpha) g(x) = f(x)$ とすると
\begin{align}
g(x) &= \frac{1}{\Phi(D + \alpha)} f(x)
\end{align}
となり、これを先の式に戻すと
\begin{align}
\frac{1}{\Phi(D)}\Big({\rm e}^{\alpha x} f(x) \Big) &= {\rm e}^{\alpha x} \frac{1}{\Phi(D + \alpha)} f(x)
\end{align}
が成り立つことが分かる。
(3)
ここで示した (2) の関係式において $\Phi(D) = D – \alpha$ とすると
\begin{align}
\frac{1}{D – \alpha}\Big({\rm e}^{\alpha x} f(x)\Big) &= {\rm e}^{\alpha x} \frac{1}{D + \alpha – \alpha} f(x) \\
&= {\rm e}^{\alpha x} \frac{1}{D} f(x)
\end{align}
が成立する。ここで $f(x)$ は任意の関数であるので ${\rm e}^{- \alpha x} f(x)$ で置き換えると
\begin{align}
\frac{1}{D – \alpha}\Big({\rm e}^{\alpha x} {\rm e}^{- \alpha x} f(x)\Big) &=
{\rm e}^{\alpha x} \frac{1}{D}\Big({\rm e}^{- \alpha x} f(x)\Big)
\end{align}
となる。ここで
\begin{align}
\frac{1}{D}\Big({\rm e}^{- \alpha x} f(x)\Big) &= \int {\rm e}^{- \alpha x} f(x) {\rm d} x
\end{align}
であることに注意すると
\begin{align}
\frac{1}{D – \alpha} f(x) &= {\rm e}^{\alpha x} \int {\rm e}^{- \alpha x} f(x) {\rm d} x
\end{align}
が成り立つことが分かる。
(4)
先に示した(2)の関係式において $\Phi(D) = (D – \alpha)^n, f(x) = 1$ とするとき
\begin{align}
\frac{1}{(D – \alpha)^n}\Big({\rm e}^{\alpha x}\Big) &= {\rm e}^{\alpha x} \frac{1}{(D + \alpha – \alpha)^n} 1 \\
&= {\rm e}^{\alpha x} \frac{1}{D^n} 1
\end{align}
が成り立つ。
ここで
\begin{align}
\int 1 {\rm d} x &= x, \\
\int x {\rm d} x &= \frac{1}{2} x^2, \\
&\cdots, \\
\int \int \cdots \int 1 ({\rm d} x)^n &= \frac{x^n}{n!}
\end{align}
が分かるので
\begin{align}
\frac{1}{(D – \alpha)^n}{\rm e}^{\alpha x} &= \frac{x^n}{n!} {\rm e}^{\alpha x}
\end{align}
が示される。