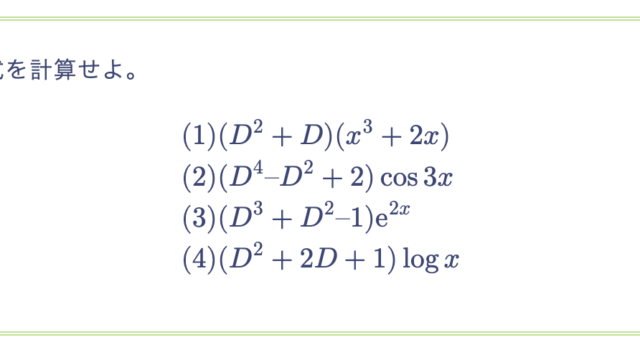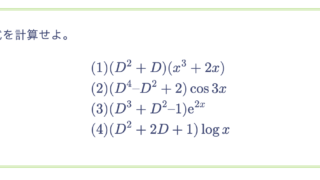次の各式が $n = 1, 2, 3, \cdots$ について成り立つことを示せ。
\begin{align}
(1)&\quad D^n {\rm e}^{\alpha x} = \alpha^n {\rm e}^{\alpha x}\\
(2)&\quad D^n \Big({\rm e}^{\alpha x} g(x)\Big) = {\rm e}^{\alpha x} \big(D + \alpha\big)^n g(x)
\end{align}
(1)
数学的帰納法で示す。
$n = 1$ の時は明らか。
$n = k$ の時に成り立つと仮定すると
\begin{align}
D^{k + 1} {\rm e}^{\alpha x} &= D \big(D^k {\rm e}^{\alpha x}\big) \\
&= D\big(\alpha^k {\rm e}^{\alpha x}\big) \\
&= \alpha^k D {\rm e}^{\alpha x} \\
&= \alpha^k \alpha {\rm e}^{\alpha x} \\
&= \alpha^{k + 1} {\rm e}^{\alpha x}
\end{align}
となり、$n = k + 1$ の時も成り立つことが分かる。
従って、数学的帰納法より、任意の $n = 1, 2, 3, \cdots$ について成り立つ。
(2)
(1) と同様に数学的帰納法で示す。
$n = 1$ の時には
\begin{align}
D\big({\rm e}^{\alpha x} g(x)\big) &= \alpha {\rm e}^{\alpha x} g(x) + {\rm e}^{\alpha x} D g(x) \\
&= \big(D + \alpha\big) \big({\rm e}^{\alpha x} g(x)\big)
\end{align}
であり、確かに成立する。$n = k$ の時に成立するとして
\begin{align}
D^{k + 1}\big({\rm e}^{\alpha x} g(x)\big) &= D D^k \big({\rm e}^{\alpha x} g(x)\big) \\
&= D \Big({\rm e}^{\alpha x} \big(D + \alpha\big)^k g(x)\Big) \\
&= \alpha {\rm e}^{\alpha x} \big(D + \alpha\big)^k g(x)
+ {\rm e}^{\alpha x} D \big(D + \alpha\big)^k g(x) \\
&= {\rm e}^{\alpha x} \big(D + \alpha\big) \big(D + \alpha)^k g(x) \\
&= {\rm e}^{\alpha x} \big(D + \alpha\big)^{k + 1} g(x)
\end{align}
となり、$n = k + 1$ の時にも成立する。従って、数学的帰納法により、任意の $n = 1, 2, 3, \cdots$ に対して成立する。