ベン図を用いた証明

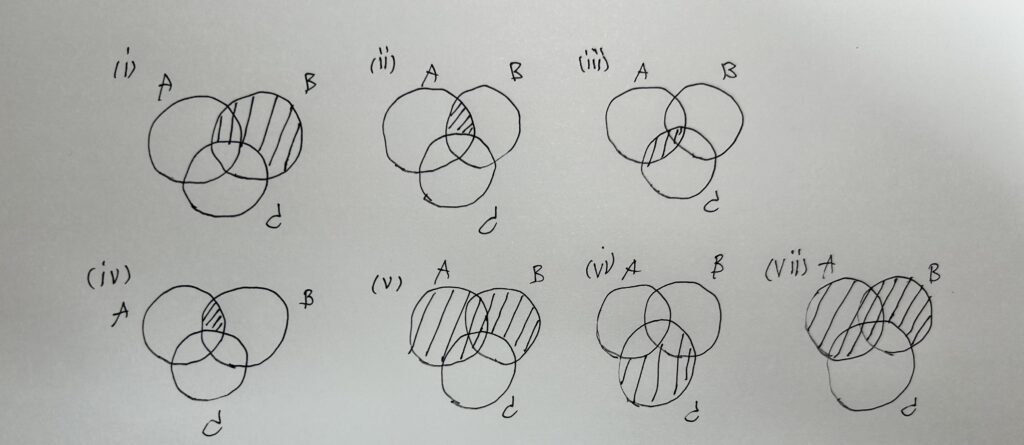
以下のように $A,B,C$ を定めるとき、$B\mathrm{\setminus }C$ は(i)の斜線部となる。

従って、$A\cap (B\mathrm{\setminus }C)$ は(ii)の斜線部となる。

また、$A\cap C$ は (iii) の斜線部となるので、$(A\cap B)\mathrm{\setminus }(A\cap C)$ は (iv) の斜線部となる。

従って $A\cap (B\mathrm{\setminus }C)=(A\cap B)\mathrm{\setminus }(A\cap C)$ が言える。

次に、$A\cup (B\mathrm{\setminus }C)$ は (v) の斜線部となる。

また、$C\mathrm{\setminus }A$ は (vi) の斜線部となるので、$A\cup (B\mathrm{\setminus }C)$ は (vii) の斜線部となる。

従って、$A\cup (B\mathrm{\setminus }C)=(A\cup B)\mathrm{\setminus }(C\mathrm{\setminus }A)$ が言える。