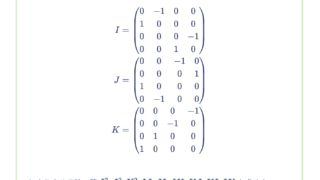
$A_{12}, A_{13}, A_{22}, A_{23}, A_{33}, B_{11}, B_{12}, B_{23}, B_{33}, C_{11}, C_{12}, C_{13}, C_{22}, C_{23}$ を $n$次正方行列、$O$ を $n$次の零行列とする。このとき、次の計算をせよ。
\begin{align}
\begin{pmatrix}
O & A_{12} & A_{13} \\
O & A_{22} & A_{23} \\
O & O & A_{33} \\
\end{pmatrix}
\begin{pmatrix}
B_{11} & B_{12} & B_{13} \\
O & O & B_{23} \\
O & O & B_{33} \\
\end{pmatrix}
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
O & C_{22} & C_{23} \\
O & O & O \\
\end{pmatrix}
\end{align}
\begin{align}
&\begin{pmatrix}
O & A_{12} & A_{13} \\
O & A_{22} & A_{23} \\
O & O & A_{33} \\
\end{pmatrix}
\begin{pmatrix}
B_{11} & B_{12} & B_{13} \\
O & O & B_{23} \\
O & O & B_{33} \\
\end{pmatrix}
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
O & C_{22} & C_{23} \\
O & O & O \\
\end{pmatrix}\\
&=
\begin{pmatrix}
O & O & A_{12}B_{23} + A_{13}B_{33} \\
O & O & A_{22}B_{23} + A_{23}B_{33} \\
O & O & A_{33}B_{33} \\
\end{pmatrix}
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
O & C_{22} & C_{23} \\
O & O & O \\
\end{pmatrix}\\
&=
\begin{pmatrix}
O & O & O \\
O & O & O \\
O & O & O \\
\end{pmatrix}
\end{align}