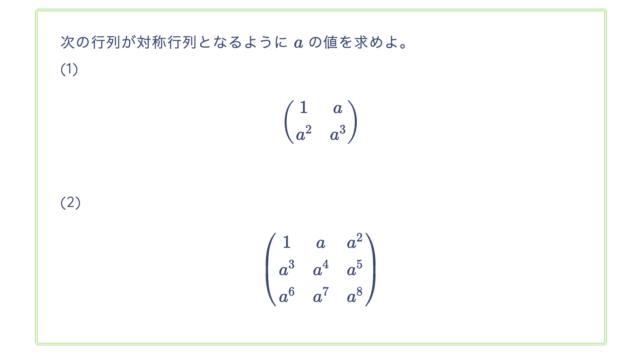
次の行列の $(i, j)$ 成分をクロネッカーのデルタを用いて表せ。
(1)
\begin{pmatrix}
1 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 3 \\
\end{pmatrix}
(2)
\begin{pmatrix}
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0 \\
\end{pmatrix}
(3)
\begin{pmatrix}
0 & 0 & 0 \\
1 & 0 & 0 \\
0 & 1 & 0 \\
\end{pmatrix}
(1)
対角成分にしか 0 でない値がないことに注意すれば
\begin{align}
a_{ij} &= i \delta_{i, j}
\end{align}
と書くことができる。
(2)
$(i, i+1)$ 成分にしか 0 でない値がないことに注意して
\begin{align}
a_{i, j} &= \delta_{i + 1, j}
\end{align}
と表すことができる。
(3)
(2) と同様に
\begin{align}
a_{i, j} &= \delta_{i, j + 1}
\end{align}
と表すことができる。