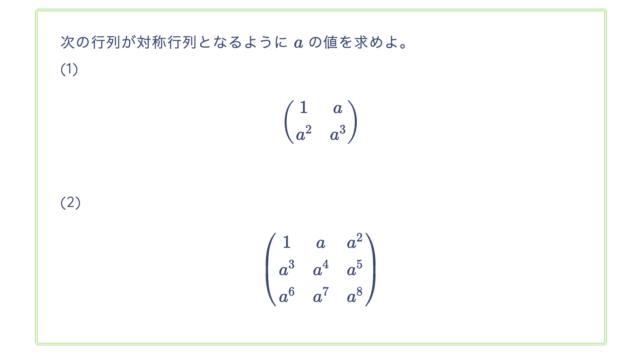
次の (1), (2) の等式が成り立つような $a, b, c$ の値を求めよ。
(1)\begin{align}
\begin{pmatrix}
a^2 + b^2 & ab + bc \\
ab + bc & b^2 + c^2 \\
\end{pmatrix} =
\begin{pmatrix}
1 & 0 \\
0 & 4 \\
\end{pmatrix}
\end{align}
(2)\begin{align}
\begin{pmatrix}
a^2 + b^2 & 1 & 2 ca \\
1 & 1 & 1 \\
2 ca & 1 & b^2 + c^2 \\
\end{pmatrix} =
\begin{pmatrix}
1 & 2 bc & 1 \\
2 bc & c^2 + a^2 & 2 ab \\
1 & 2 ab & 1 \\
\end{pmatrix}
\end{align}
(1)
(1, 2) 成分と(2, 1) 成分は同じ条件を導き
\begin{align}
b (a + c) = 0
\end{align}
を得る。ここで、$b = 0$ または $c = – a$ が得られるが、後者は解として不適である。
なぜなら、(1, 1) 成分から $a^2 + b^2 = 1$ が得られ、同時に (2, 2) 成分から $b^2 + c^2 = b^2 + a^2 = 4$ が得られるからである。
従って、$b = 0$ が得られる。
このとき、(1, 1) 成分から $a^2 = 1$が得られ、(2, 2)成分から $c^2 = 4$ が得られる。
従って
\begin{align}
a = \pm 1, b = 0, c = \pm 2
\end{align}
が解となる。ここで複合は任意の組み合わせを取る。
(2)
各成分を比較して、次の6つの式が得られる。
\begin{align}
a^2 + b^2 &= 1 \\
c^2 + a^2 &= 1 \\
b^2 + c^2 &= 1 \\
2 b c &= 1 \\
2 c a &= 1 \\
2 a b &= 1
\end{align}
これらの式より
\begin{align}
(a – b)^2 &= 0 \\
(c – a)^2 &= 0 \\
(b – c)^2 &= 0
\end{align}
が得られるので、$a = b = c$ が導かれる。
従って
\begin{align}
a = b = c = \pm \frac{1}{\sqrt{2}}
\end{align}
が解となる。