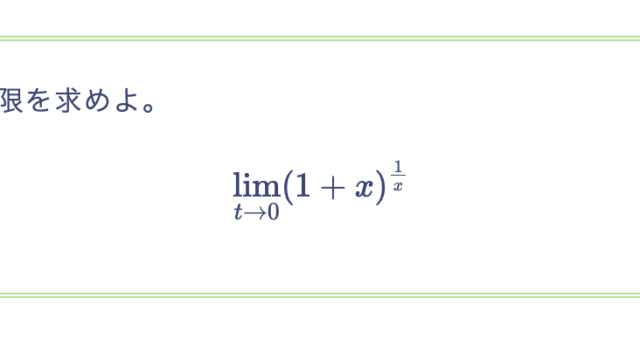関数 $|x|$ は $x = 0$ で連続であることを示せ。
$f(x) = |x|$ とするとき、$f(0) = |0| = 0$ であり
\begin{align}
\lim_{x \to 0+} f(x) &= \lim_{x \to 0+} x \\
&= 0 \\
\lim_{x \to 0-} f(x) &= \lim_{x \to 0-} (-x) \\
&= 0
\end{align}
が成り立つので、関数 $|x|$ は $x = 0$ で連続であることが分かる。