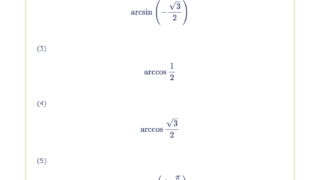
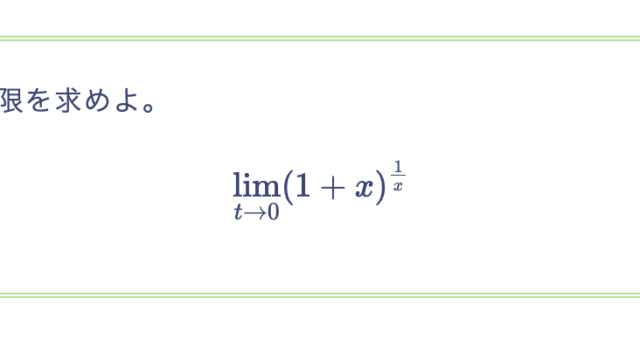次の方程式は、与えられた区間で解を持つことを示せ。
(1) $x^3 – 4 x + 1 = 0\ (0, 1)$
(2) $x = \sin x + 1/2\ (\pi/4, \pi/2)$
(1)
$f(x) = x^3 – 4 x + 2$ とおくとき、$f(0) = 2, f(1) = -1$ となる。
従って、中間値の定理より $f(x) = 0$ となる $x$ が $0 < x < 1$ に少なくとも1つ存在する。
(2)
$f(x) = x \sin x – 1/2$ とおくとき、$f(\pi/4) = \pi/4 – \sqrt{2}/2 – 1/2 < 0, f(\pi/2) = \pi/2 - 1/2 > 0$ となる。
従って、中間値の定理より $f(x) = 0$ となる $x$ が $\pi/4 < x < \pi/2$ に少なくとも1つ存在する。