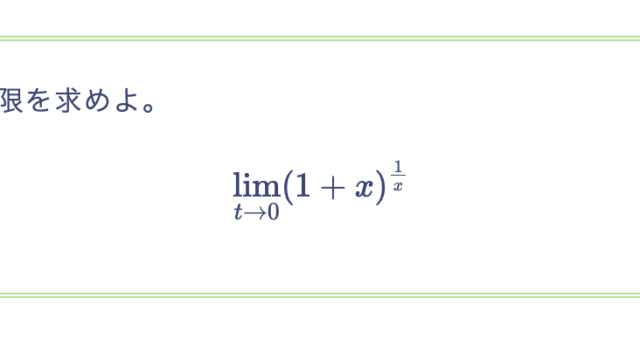関数 $f(x)$ は $\mathbb{R}$ で定義され、$f(2 x) = f(x)$ を満たすとする。$f(x)$ が $x = 0$ で連続であるとき、$f(x) = c$ (定数)であることを示せ。
$\forall x \in \mathbb{R}$ について
\begin{align}
\lim_{n \to \infty} \frac{x}{2^n} &= 0
\end{align}
であることに注意する。今、条件より $f(2 x) = f(x)$ であるので
\begin{align}
f(x) = f\left(\frac{x}{2}\right) = \cdots = f\left(\frac{x}{2^n}\right)
\end{align}
が成り立つ。
ここで $f(x)$ は $x = 0$ で連続であるので
\begin{align}
f(x) &= \lim_{n \to \infty} f\left(\frac{x}{2^n}\right) = f(0)
\end{align}
となり、$f(x)$ は定数であることが分かる。