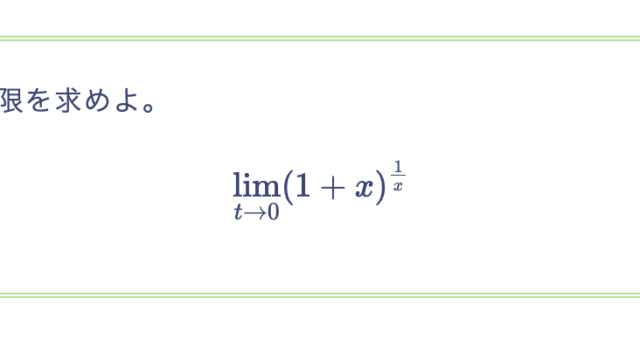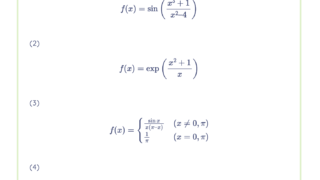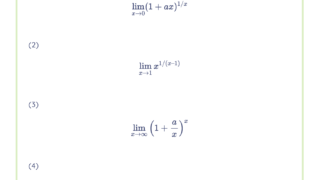関数の極限(3)

$x > 1$ に対して $n \in \mathbb{N}$ を $n \le x < n + 1$ と取ると、$x \to \infty$ とするとき $n \to \infty$ となる。この時 \begin{align} \left(1 + \frac{1}{n + 1}\right)^n \le \left(1 + \frac{1}{x}\right)^x \le \left(1 + \frac{1}{n}\right)^{n + 1} \end{align} が成り立ち、不等式の左右は各々 $n \to \infty$ で ${\rm e}$ に収束するので、はさみうちの原理より \begin{align} \lim_{x \to \infty}\left(1 + \frac{1}{x}\right)^x = {\rm e} \end{align} が示される。 次に、$x \to - \infty$ の時には $t = - x$ として \begin{align} \lim_{x \to - \infty} \left(1 + \frac{1}{x}\right)^x &= \lim_{t \to \infty}\left(1 - \frac{1}{t}\right)^{- t} \\ &= \lim_{t \to \infty} \left(1 + \frac{1}{t - 1}\right)^{t - 1}\left(1 + \frac{1}{t - 1}\right) \\ &= {\rm e} \end{align} が言える。 最後に $t = 1/x$ として \begin{align} \lim_{x \to +0}(1 + x)^{1/x} &= \lim_{t \to \infty}\left(1 + \frac{1}{t}\right)^t = {\rm e} \\ \lim_{x \to -0}(1 + x)^{1/x} &= \lim_{t \to - \infty}\left(1 + \frac{1}{t}\right)^t = {\rm e} \end{align} より \begin{align} \lim_{x \to 0} (1 + x)^{1/x} = {\rm e} \end{align} が示される。