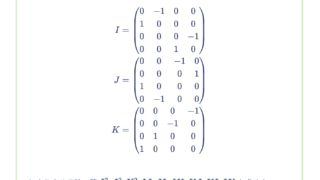
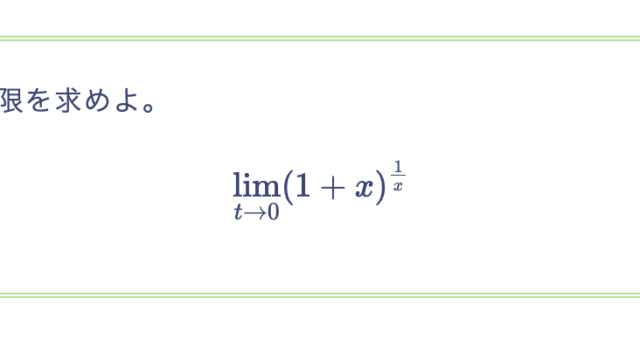関数 $f(x), g(x)$ に対して、$\lim_{n \to \infty}f(x) = \infty$ であり、ある $c \in \mathbb{R}$ に対して、$g(x) \ge c$ であるとすると
\begin{align}
\lim_{x \to \infty} (f(x) + g(x)) = \infty
\end{align}
が成り立つ。このことを用いて
\begin{align}
\lim_{x \to \infty}\frac{x^2 – \sin^2 x}{x – \sin x}
\end{align}
を求めよ。
極限を求める関数は
\begin{align}
\frac{x^2 – \sin^2 x}{x – \sin x} &= x + \sin x
\end{align}
と変形できることに注意して
\begin{align}
\lim_{x \to \infty} x &= \infty \\
\sin x &\ge -1
\end{align}
が成り立つことを考慮すると、問題で与えられた条件において $f(x) = x, g(x) = \sin x, c = – 1$ が成立するので
\begin{align}
\lim_{x \to \infty}\frac{x^2 – \sin^2 x}{x – \sin x} &= \infty
\end{align}
が言える。