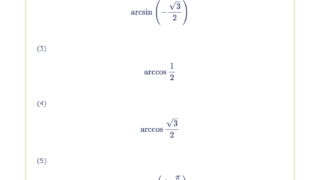
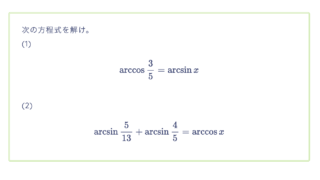
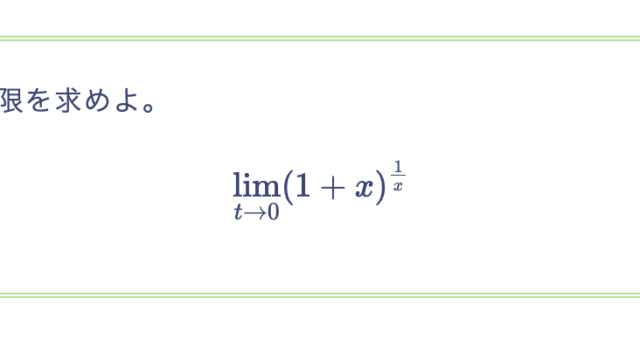次の示せ。
(1)
\begin{align}
\lim_{x \to 0} \frac{\log(1 + x)}{x} = 1 \\
\end{align}
(2)
\begin{align}
\lim_{x \to 0} \frac{{\rm e}^x – 1}{x} = 1 \\
\end{align}
(3)
\begin{align}
\lim_{x \to 0} \frac{{\rm e}^x – {\rm e}^{- x}}{x} = 2
\end{align}
(1)
\begin{align}
\lim_{x \to 0} \frac{\log(1 + x)}{x} &= \lim_{x \to 0} \log(1 + x)^{\frac{1}{x}} \\
&= \log{\rm e} \\
&= 1
\end{align}
(2)
$t = {\rm e}^x – 1$ とおくと、$x \to 0$ の時 $t \to 0$ であるので
\begin{align}
\lim_{x \to 0} \frac{{\rm e}^x – 1}{x} &= \lim_{t \to 0} \frac{t}{\log(1 + t)} \\
&= 1
\end{align}
(3)
\begin{align}
\lim_{x \to 0} \frac{{\rm e}^x – {\rm e}^{- x}}{x} &=
\lim_{x \to 0} \left(\frac{{\rm e}^x – 1}{x} + \frac{1 – {\rm e}^{- x}}{x}\right) \\
&= \lim_{x \to 0} \left(\frac{{\rm e}^x – 1}{x} + \frac{{\rm e}^x – 1}{x} {\rm e}^{- x}\right) \\
&= 1 + 1 \\
&= 2
\end{align}