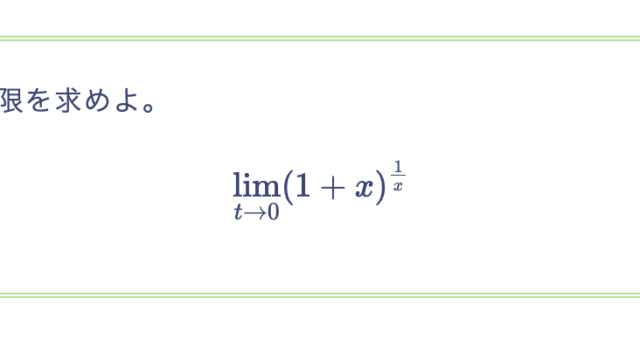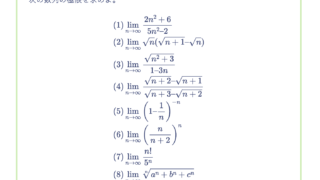次の数列 $\{a_n\}$ が極限値を持つか調べ、極限値を持つならば、その極限値を求めよ。
\begin{align}
(1) & a_n = 3 + (-1)^n \frac{1}{n} \\
(2) & a_n = \sin(n \pi) \\
(3) & a_n = 2 + (-1)^n 2 \\
(4) & a_n = \frac{1 – 3 + 5 – \cdots + (-1)^{n + 1}(2 n – 1)}{n}
\end{align}
(1) 数列 $\{a_n\}$ は極限値 3 を持つ。なんとなれば
\begin{align}
|a_n – 3| &= |(-1)^n \frac{1}{n}| \\
&= \frac{1}{n}
\end{align}
となり、$\frac{1}{n} \to 0\ (n \to \infty)$ となるからである。
(2) 数列 $\{a_n\}$ は極限値を持たない。なんとなれば、$n \in \mathbb{N}$ とするとき
\begin{align}
a_n &= 0\ (n:{\rm odd\ numbers}) \\
a_n &= 4\ (n:{\rm even\ numbers})
\end{align}
となるからである。
(3) 数列 $\{a_n\}$ は極限値を持たない。なんとなれば、$k \in \mathbb{Z}$ とするとき
\begin{align}
a_n &= 0\ (n = 2k, 2k – 1) \\
a_n &= 1\ (n = 2k + 1/2) \\
a_n &= -1\ (n = 2k + 3/2)
\end{align}
となるからである。
(4) 数列 $\{a_n\}$ は極限値を持たないことが次のようにして分かる。
まず
\begin{align}
A_n &= 1 – 3 + 5 – \cdots +(-1)^{n + 1}(2 n – 1)
\end{align}
と定める時、$A_n = (-1)^{n + 1} n$ となることが、数学的帰納法によって示される。
実際に、$n = 1$ のときは $A_0 = 1$ となり成り立っている。
$n = k$ のとき成立していると仮定すると
\begin{align}
A_{k + 1} &= A_k + (-1)^{k + 2}(2 (k + 1) – 1) \\
&= (-1)^{k + 1} k + (-1)^k(2 k + 1) \\
&= (-1)^k( – k + 2 k + 1) \\
&= (-1)^{k + 1 + 1}(k + 1)
\end{align}
となり、$n = k + 1$ の時も成り立っていることが分かる。
これより
\begin{align}
a_n &= \frac{A_n}{n} \\
&= (-1)^{n + 1}
\end{align}
となり、これは
\begin{align}
a_n &= 1\ (n:{\rm odd numbers}) \\
a_n &= -1\ (n:{\rm even numbers})
\end{align}
となり、極限値を持たないことが分かる。