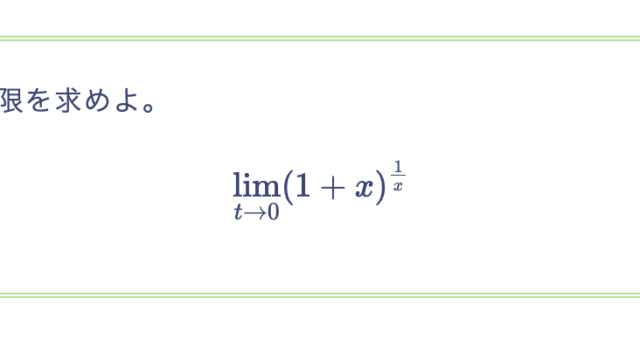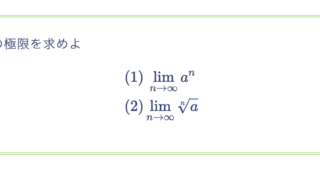次の数列の極限を求めよ。
\begin{align}
(1) & \lim_{n \to \infty} \frac{2 n^2 + 6}{5 n^2 – 2} \\
(2) & \lim_{n \to \infty} \sqrt{n}(\sqrt{n + 1} – \sqrt{n})\\
(3) & \lim_{n \to \infty} \frac{\sqrt{n^2 + 3}}{1 – 3 n} \\
(4) & \lim_{n \to \infty} \frac{\sqrt{n + 2} – \sqrt{n + 1}}{\sqrt{n + 3} – \sqrt{n + 2}} \\
(5) & \lim_{n \to \infty}\left(1 – \frac{1}{n}\right)^{-n} \\
(6) & \lim_{n \to \infty}\left(\frac{n}{n + 2}\right)^n \\
(7) & \lim_{n \to \infty} \frac{n!}{5^n} \\
(8) & \lim_{n \to \infty} \sqrt[n]{a^n + b^n + c^n}
\end{align}
(1)
\begin{align}
\lim_{n \to \infty} \frac{2 n^2 + 6}{5 n^2 – 2} &=
\lim_{n \to \infty} \frac{2 + 6/n^2}{5 – 2/n^2} \\
&= \frac{2}{5}
\end{align}
(2)
\begin{align}
\lim_{n \to \infty} \sqrt{n}(\sqrt{n + 1} – \sqrt{n}) &=
\lim_{n \to \infty} \frac{\sqrt{n}(\sqrt{n + 1} – \sqrt{n})(\sqrt{n + 1} + \sqrt{n})}{(\sqrt{n + 1} + \sqrt{n}} \\
&= \lim_{n \to \infty} \frac{\sqrt{n}}{\sqrt{n + 1} + \sqrt{n}} \\
&= \frac{1}{2}
\end{align}
(3)
\begin{align}
\lim_{n \to \infty} \frac{\sqrt{n^2 + 3}}{1 – 3 n} &=
\lim_{n \to \infty} \frac{\sqrt{1 + 3/n^2}}{1/n – 3} \\
&= – \frac{1}{3}
\end{align}
(4)
\begin{align}
\lim_{n \to \infty} \frac{\sqrt{n + 2} – \sqrt{n + 1}}{\sqrt{n + 3} – \sqrt{n + 2}}&=
\lim_{n \to \infty} \frac{\sqrt{n + 2} – \sqrt{n + 1}}{\sqrt{n + 3} – \sqrt{n + 2}}
\frac{\sqrt{n + 3} + \sqrt{n + 2}}{\sqrt{n + 3} + \sqrt{n + 2}}
\frac{\sqrt{n + 2} + \sqrt{n + 1}}{\sqrt{n + 2} + \sqrt{n + 1}} \\
&= \lim_{n \to \infty} \frac{\sqrt{n + 3} + \sqrt{n + 2}}{\sqrt{n + 2} + \sqrt{n + 1}} \\
&= 1
\end{align}
(5)
\begin{align}
\lim_{n \to \infty}\left(1 – \frac{1}{n}\right)^{-n} &=
\lim_{n \to \infty} \frac{1}{\left(1 – \frac{1}{n}\right)^n} \\
&= \lim_{n \to \infty} \left(\frac{n}{n – 1}\right)^n \\
&= \lim_{n \to \infty} \left(1 + \frac{1}{n – 1}\right)\left(1 + \frac{1}{n – 1}\right)^{n – 1} \\
&= e
\end{align}
(6)
\begin{align}
\lim_{n \to \infty}\left(\frac{n}{n + 2}\right)^n &=
\lim_{n \to \infty} \left(\frac{1}{\left(1 + \frac{2}{n}\right)^{\frac{n}{2}}}\right)^2 \\
&= \frac{1}{e^2}
\end{align}
(7)
\begin{align}
C = \frac{5!}{5^5}
\end{align}
とすると、$n \le n$ のとき
\begin{align}
\frac{n!}{5^n} &= \frac{5!}{5^5}\frac{6\cdot 6 \cdot \cdots \cdot n}{5^{n – 5}} \\
\ge C \left(\frac{6}{5}\right)^{n – 5}
\end{align}
が成り立つ。ここで、先の問題の答えより、これは発散することが分かる。
(8)
\begin{align}
M = {\rm max}\{a, b ,c\}
\end{align}
とするとき
\begin{align}
M^n \le a^n + b^n + c^n \le 3 M^n
\end{align}
が言えるので
\begin{align}
M \le \sqrt[n]{a^n + b^n + c^n} \le \sqrt[n]{3} M
\end{align}
が成り立ち、$n \to \infty$ とするとき、先の問題の答えと、はさみうちの原理より、これは $M$ に収束する。
すなわち
\begin{align}
\lim_{n \to \infty}\sqrt[n]{a^n + b^n + c^n} = {\rm max}\{a, b, c\}
\end{align}
が示される。