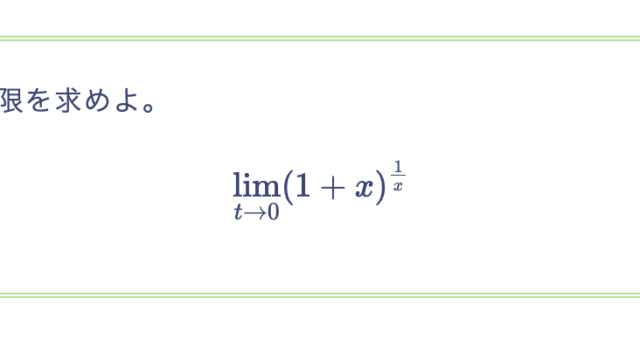$f(x)$ を有界閉区間 $[a, b]$ で連続な関数とする。任意の $x \in [a, b]$ に対して $f(x) \in [a, b]$ が成り立つとき、$f(c) = c$ となる $c \in [a, b]$ が存在することを示せ。
関数 $g(x)$ を
\begin{align}
g(x) &= x – f(x)
\end{align}
と定める。このとき、関数 $g(x)$ は $[a, b]$ で連続である。
また、$f(x) \in [a, b]$ より、$g(a) \le 0, g(b) \ge 0$ となる。
もしも、$g(a) = 0$ または $g(b) = 0$ のときには、各々 $c = a, c= b$ とおけば、$f(c) = c$ を満たすことが分かる。
$g(a) \neq 0$ かつ $g(b) \neq 0$ のとき、すなわち、$g(a) < 0$ かつ $g(b) > 0$ のとき、中間値の定理により、$g(c) = 0$ となる $c \in (a, b)$ が存在する。このような $c$ に対して、$f(c) = c$ が成り立つ。
従って、題意が示された。