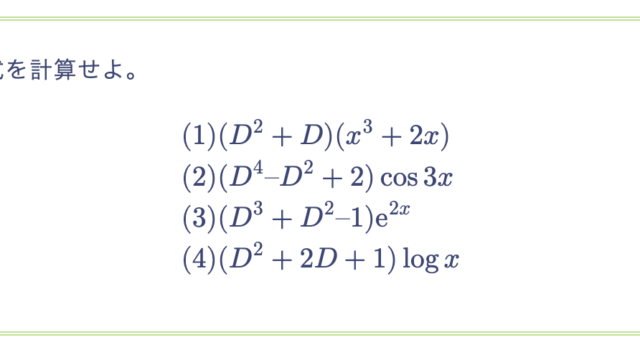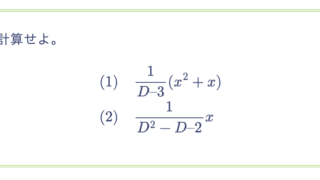逆演算子の性質(2)

\begin{align}
y = \frac{1}{1 – D} f(x)
\end{align}
とおくと、これは
\begin{align}
(1 – D) y &= f(x)
\end{align}
なる微分方程式と等価である。これを変形して
\begin{align}
y &= f(x) + Dy
\end{align}
が得られる。この右辺の $y$ を逐次左辺の $y$ だと思って代入していくと
\begin{align}
y &= f(x) + D(f(x) + D y) \\
&= f(x) + D f(x) + D^2 y \\
&= f(x) + D f(x) + D^2(f(x) + D y) \\
&= f(x) + D f(x) + D^2 f(x) + D^3 y \\
& \cdots \\
&= f(x) + D f(x) + D^2 f(x) + \cdots + D^n f(x) + D^{n + 1} y
\end{align}
ここで、$f(x)$ は $n$ 次の多項式であるので、最後の式の最後の項 $D^{n + 1} y$ はゼロである。

従って
\begin{align}
y & = (1 + D + D^2 + \cdots + D^n) f(x) \\
\frac{1}{1 – D} f(x) &= (1 + D + D^2 + \cdots + D^n) f(x)
\end{align}
が成り立つ。

(注)
この性質は $\frac{1}{1 – x}$ のテイラー展開が
\begin{align}
\frac{1}{1 – x} &= 1 + x + x^2 + \cdots
\end{align}
であることから、$x$ を $D$ と置き換えて、$f(x)$ が $n$ 次多項式であることを考慮して $D^{n + 1} f(x) = 0$ であることを使うと、自然な性質であると解釈出来る。

なお、このテイラー展開は、初項 1 公比 x の無限等比級数の和と思えば、すぐに導かれる。