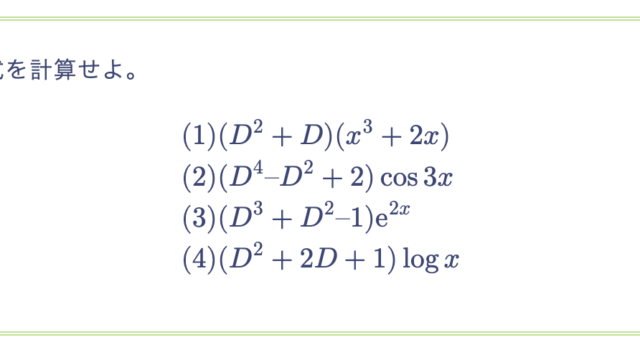定数係数非同次微分方程式(1)

(1)

解くべき微分方程式は、微分演算子
\begin{align}
\Phi_1(D) &= D^2 + 8 D + 16
\end{align}
を用いて
\begin{align}
\Phi_1(D) y &= 4 {\rm e}^{- 2 x}
\end{align}
と表すことが出来る。この微分方程式の余関数 $Y$ は、この微分方程式の特性方程式
\begin{align}
\Phi_1(\lambda) &= 0
\end{align}
を解いて
\begin{align}
\Phi_1(\lambda) &= \lambda^2 + 8 \lambda + 16 \\
&= (\lambda + 4)^2
\end{align}
から、$\lambda = – 4\ ({\text 重解})$ となるので
\begin{align}
Y &= (C_1 + C_2 x) {\rm e}^{- 4 x}
\end{align}
と求まる。ここに $C_1, C_2$ は共に任意の定数である。

解くべき微分方程式の特殊解 $y_0$ は、先の結果を用いて
\begin{align}
y_0 &= \frac{1}{\Phi(D)} 4 {\rm e}^{- 2 x} \\
&= 4 \frac{1}{(D + 4)^2} {\rm e}^{- 2 x} \\
&= 4 \frac{{\rm e}^{- 2 x}}{(- 2 + 4)^2} \\
&= {\rm e}^{- 2 x}
\end{align}
と求まる。従って、一般解は
\begin{align}
y &= {\rm e}^{- 2 x} + (C_1 + C_2 x) {\rm e}^{- 4 x}
\end{align}
と求まる。

(2)

解くべき微分方程式は、微分演算子
\begin{align}
\Phi_2(D) &= D^2 + 1
\end{align}
を用いて
\begin{align}
\Phi_2(D) y &= \sin 2 y
\end{align}
と書くことが出来る。この微分方程式の余関数 $Y$ は、同伴方程式の特性方程式を解いて
\begin{align}
\Phi_2(\lambda) &= \lambda^2 + 1 = 0
\end{align}
より $\lambda = \pm i$ であるので
\begin{align}
Y &= C_1 \cos x + C_2 \sin x
\end{align}
と求まる。特殊解 $y_0$ は、先の結果を用いて
\begin{align}
y_0 &= \frac{1}{\Phi_2(D)} \sin 2 x \\
&= \frac{1}{D^2 + 1} \sin 2 x \\
&= \frac{\sin 2 x}{- 2^2 + 1} \\
&= – \frac{1}{3} \sin 2 x
\end{align}
となる。従って、一般解は
\begin{align}
y &= – \frac{1}{3} \sin 2 x + C_1 \cos x + C_2 \sin x
\end{align}
と求まる。

(3)

求める微分方程式は微分演算子
\begin{align}
\Phi_3(D) &= D^2 – 3 D + 2
\end{align}
を用いて
\begin{align}
\Phi_3(D) y &= x {\rm e}^x
\end{align}
と書くことが出来る。この微分方程式の余関数 $Y$ は、同伴方程式を解いて
\begin{align}
\Phi_3(\lambda) &= \lambda^2 – 3 \lambda + 2 \\
&= (\lambda – 1) (\lambda – 2)
\end{align}
より $\lambda = 1, 2$ であるので
\begin{align}
Y &= C_1 {\rm e}^x + C_2 {\rm e}^{2 x}
\end{align}
と求まる。解くべき微分方程式の特殊解 $y_0$ は、先の結果を用いて
\begin{align}
y_0 &= \frac{1}{\Phi_3(D)} x {\rm e}^x \\
&= \frac{1}{(D – 2) (D – 1)} x {\rm e}^x \\
&= \frac{1}{D – 2} {\rm e}^x \int {\rm e}^{- x} x {\rm e}^x {\rm d} x \\
&= \frac{1}{D – 2} {\rm e}^x \int x {\rm d} x \\
&= \frac{1}{2} \frac{1}{D – 2} x^2 {\rm e}^x \\
&= \frac{1}{2} {\rm e}^{2 x} \int {\rm e}^{- 2 x} x^2 {\rm e}^x {\rm d} x \\
&= – \frac{1}{2} (x^2 + 2 x + 2) {\rm e}^x
\end{align}
と求まる。従って、求める微分方程式の一般解は
\begin{align}
y &= – \frac{1}{2}(x^2 + 2 x + 2) {\rm e}^x + C_1 {\rm e}^x + C_2 {\rm e}^{2 x}
\end{align}
と求まる。

(4)

解くべき微分方程式は、微分演算子
\begin{align}
\Phi_4(D) &= D^2 + 2 D + 1
\end{align}
を用いて
\begin{align}
\Phi_4(D) y &= {\rm e}^{- x} \cos x
\end{align}
と表すことが出来る。この微分方程式の余関数 $Y$ は、その同伴方程式を解いて
\begin{align}
\Phi_4(\lambda) &= \lambda^2 + 2 \lambda + 1 \\
&= (\lambda + 1)^2
\end{align}
より
\begin{align}
Y &= (C_1 + C_2 x) {\rm e}^{- x}
\end{align}
と求まる。解くべき微分方程式の特殊解 $y_0$ は、先の結果を用いて
\begin{align}
y_0 &= \frac{1}{\Phi_4(D)} {\rm e}^{- x} \cos x \\
&= \frac{1}{(D + 1)^2} {\rm e}^{- x} \cos x \\
&= {\rm e}^{- x} \frac{1}{(D – 1 + 1)^2} \cos x \\
&= {\rm e}^{- x} \frac{1}{D^2} \cos x \\
&= {\rm e}^{- x} \int \int \cos x {\rm d}x {\rm d} x \\
&= – {\rm e}^{- x} \cos x
\end{align}
となるので、一般解は
\begin{align}
y &= (- \cos x + C_1 + C_2 x) {\rm e}^{- x}
\end{align}
と求まる。