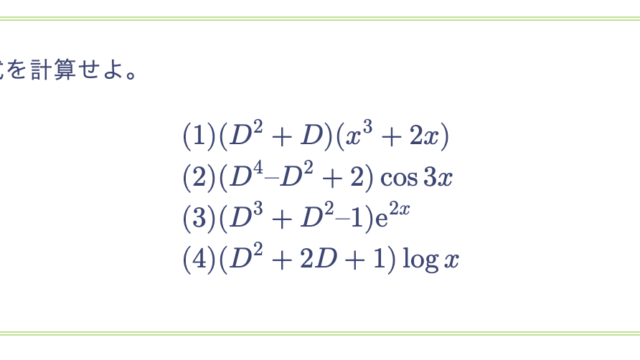定数係数連立微分方程式(2)

先ず、第3式は、定数係数非同次微分方程式であるので、$y$ の一般解を求めることが出来る。

同伴方程式 $(D^2 + 2)y = 0$ の特性方程式 $\lambda^2 + 2 = 0$ を解いて
\begin{align}
\lambda = \pm \sqrt{2} i
\end{align}
が得られるので、余関数 $Y$ は
\begin{align}
Y &= C_1 \cos \sqrt{2} x + C_2 \sin \sqrt{2} x
\end{align}
と求まる。また、特殊解 $y_0$ を求めると
\begin{align}
y_0 &= \frac{1}{D^2 + 2} \cos x \\
&= \frac{\cos x}{- 1^2 + 2} \\
&= \cos x
\end{align}
となる。従って、$y$ の一般解は
\begin{align}
y &= \cos x + C_1 \cos \sqrt{2} x + C_2 \sin \sqrt{2} x
\end{align}
と求まる。

これを第2式に代入して
\begin{align}
(D^2 – 1) z &= y \\
&= \cos x + C_1 \cos \sqrt{2} x + C_2 \sin \sqrt{2} x
\end{align}
が得られるので、この微分方程式を解けば $z$ が得られる。この微分方程式の
同伴方程式 $(D^2 – 1) z = 0$ の特性方程式 $\lambda^2 – 1 = 0$ を解くと
\begin{align}
\lambda = \pm 1
\end{align}
が得られる。従って、余関数 $Z$ は
\begin{align}
Z &= C_3 {\rm e}^{- x} + C_4 {\rm e}^x
\end{align}
と求まる。特殊解 $z_0$ は
\begin{align}
z_0 &= \frac{1}{D^2 – 1}\big(\cos x + C_1 \cos \sqrt{2} x + C_2 \sin \sqrt{2} x\big) \\
&= \frac{1}{D^2 – 1} \cos x + C_1 \frac{1}{D^2 – 1} \cos \sqrt{2} x
+ C_2 \frac{1}{D^2 – 1} \sin \sqrt{2} x \\
&= \frac{\cos x}{- 1^2 – 1} + C_1 \frac{\cos \sqrt{2} x}{- (\sqrt{2})^2 – 1}
+ C_2 \frac{\sin \sqrt{2} x}{- (\sqrt{2})^2 – 1} \\
&= – \frac{1}{2} \cos x – \frac{C_1}{3} \cos \sqrt{2} x – \frac{C_2}{3} \sin \sqrt{2} x
\end{align}
と求められる。従って、一般解 $z$ は
\begin{align}
z &= – \frac{1}{2} \cos x – \frac{C_1}{3} \cos \sqrt{2} x – \frac{C_2}{3} \sin \sqrt{2} x
+ C_3 {\rm e}^{- x} + C_4 {\rm e}^x
\end{align}
と求まる。

最後に、ここまでで得られた $z, y$ を第1式に代入して
\begin{align}
(D^2 + 1) w &= y + 3 z \\
&= \cos x + C_1 \cos \sqrt{2} x + C_2 \sin \sqrt{2} x \\
& \quad + 3 \bigg(- \frac{1}{2} \cos x – \frac{C_1}{3} \cos \sqrt{2} x – \frac{C_2}{3} \sin \sqrt{2} x
+ C_3 {\rm e}^{- x} + C_4 {\rm e}^x\bigg) \\
&= – \frac{1}{2} \cos x + 3 C_3 {\rm e}^{- x} + 3 C_4 {\rm e}^x
\end{align}
が得られる。この微分方程式の同伴方程式 $(D^2 + 1) w = 0$ の特性方程式 $\lambda^2 + 1 = 0$ を解いて
\begin{align}
\lambda &= \pm i
\end{align}
が得られるので、余関数 $W$ は
\begin{align}
W &= C_5 \cos x + C_6 \sin x
\end{align}
と求められる。特殊解 $z_0$ は
\begin{align}
z_0 &= \frac{1}{D^2 + 1} \bigg(- \frac{1}{2} \cos x + 3 C_3 {\rm e}^{- x} + 3 C_4 {\rm e}^{x}\bigg) \\
&= – \frac{1}{2} \frac{x \sin x}{2} + 3 C_3 \frac{{\rm e}^{- x}}{(-1)^2 + 1}
+ 3 C_4 \frac{{\rm e}^{x}}{1^2 + 1} \\
&= – \frac{1}{4} x \sin x + \frac{3}{2} C_3 {\rm e}^{- x} + \frac{3}{2} C_4 {\rm e}^x
\end{align}
と求められる。従って、一般解 $w$ は
\begin{align}
w &= – \frac{1}{4} x \sin x + \frac{3}{2} C_3 {\rm e}^{- x} + \frac{3}{2} C_4 {\rm e}^x
+ C_5 \cos x + C_6 \sin x
\end{align}
と求まる。

これで、$y, z, w$ の全ての一般解が得られた。

なお、$y, z, w$ の各々に対して2階の微分方程式であったので、各々2つずつの任意定数が必要であり、
最終的な答えには $C_1, \cdots, C_6$ の6つの任意定数が表れている。