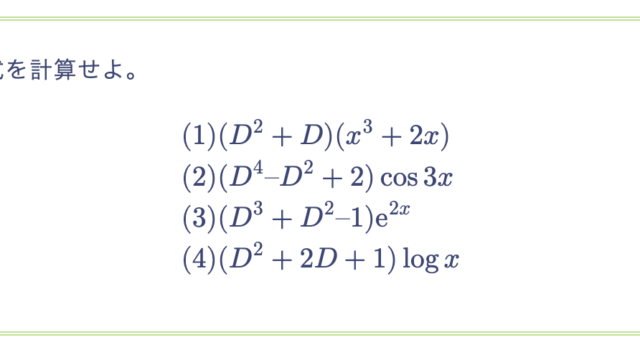定数係数連立微分方程式(1)

(1)

先ず、未知関数 $z$ を消去する。
\begin{align}
\begin{cases}
(D – 3)(D – 1) y – (D – 3) z = 0 \\
y + (D – 3) z = 0
\end{cases}
\end{align}
から
\begin{align}
\big((D – 3) (D – 1) y + 1\big) y &= 0 \\
(D^2 – 4 D + 4)y & = 0 \\
(D – 2)^2 y &= 0
\end{align}
この微分方程式の特性方程式 $(\lambda – 2)^2 = 0$ より、$\lambda = 2$ (重解)が得られるので、一般解 $y$ は
\begin{align}
y = (C_1 + C_2 x) {\rm e}^{2 x}
\end{align}
が得られる。

さらに $z = (D – 1)y$ より
\begin{align}
z &= (D – 1) (C_1 + C_2 x) {\rm e}^{2 x} \\
&= (C_1 + C_2 + C_2 x){\rm e}^{2 x}
\end{align}
と求まる。結局、求める一般解は
\begin{align}
\begin{cases}
y = (C_1 + C_2 x) {\rm e}^{2 x} \\
z = (C_1 + C_2 + C_2 x) {\rm e}^{2 x}
\end{cases}
\end{align}
となる。

(2)

先ず、未知関数 $z$ を消去する。
\begin{align}
\begin{cases}
(D – 3)(D – 1) y – (D – 3) z = (D – 3)(x^2) = 2 x – 3 x^2 \\
y + (D – 3)z = 3 x^2
\end{cases}
\end{align}
より
\begin{align}
\big((D – 3)(D – 1) + 1\big) y &= 2 x \\
(D – 2)^2 y &= 2x
\end{align}
が得られる。この同伴方程式 $(D – 2)^2 y = 0$ の特性方程式 $(\lambda – 2)^2 = 0$ を解いて、
$\lambda = 2$ (重解)が得られる。従って、先の微分方程式の余関数 $Y$ は
\begin{align}
Y &= (C_1 + C_2 x) {\rm e}^{2 x}
\end{align}
と求まる。さらに、特殊解 $y_0$ は
\begin{align}
y_0 &= \frac{1}{D^2 – 4 D + 4} 2x \\
&= \frac{1}{4}\frac{1}{1 – \frac{4 D – D^2}{4}} 2 x \\
&= \frac{1}{4}\big(1 + \frac{4 D – D^2}{4}\big) 2 x \\
&= \frac{1}{2}(x + 1)
\end{align}
と求まる。
従って、一般解 $y$ は
\begin{align}
y &= \frac{1}{2} + \frac{1}{2} x + (C_1 + C_2 x) {\rm e}^{2 x}
\end{align}
となる。

さらに
\begin{align}
z &= (D – 1) y – x^2 \\
&= (D – 1)\bigg(\frac{1}{2} x + \frac{1}{2} + (C_1 + C_2 x) {\rm e}^{2 x}\bigg) – x^2 \\
&= – x^2 – \frac{1}{2} x + (C_1 + C_2 + C_2 x) {\rm e}^{2 x}
\end{align}
と求まる。結局、求める一般解は
\begin{align}
\begin{cases}
y = \frac{1}{2}x + \frac{1}{2} + (C_1 + C_2 x) {\rm e}^{2 x} \\
z = – x^2 – \frac{1}{2} x + (C_1 + C_2 x) {\rm e}^{2 x}
\end{cases}
\end{align}
となる。